专利摘要

本发明公开了一种微机电系统(MEMS)系统级设计中的变截面梁建模方法，属于微机电系统设计领域。该方法的主要过程为：首先建立变截面梁的局部坐标系，然后根据结构力学和结构矩阵分析理论分别推导出局部坐标系下变截面梁刚度矩阵、阻尼矩阵和质量矩阵，并利用这些矩阵建立变截面梁的二阶动力学方程，最后利用硬件描述语言对二阶动力学方程进行编码，实现变截面梁的参数化系统级组件建模。本发明提出的针对宽度随长度方向线性变化的变截面梁的系统级建模方法，解决了当前对具有此种结构的MEMS器件无法进行系统级仿真设计的问题。

说明书

技术领域

本发明涉及微机电系统(MEMS)系统级设计中的一种变截面梁建模方法，属于微机电系统设计领域。

背景技术

在MEMS结构中，为了实现梁的某些设计目标，如应力集中小、体积小、强度高、重量轻、稳定性佳等，并且考虑梁所受弯矩的大小沿轴线变化时，常采用宽度随长度线性变化的变截面梁代替常规的等截面梁来优化结构。如在微加速度计、微机械陀螺等惯性器件中，绝大多数悬臂梁所承受的弯矩都是沿其轴向变化的，因此必须保证悬臂梁结构自由端具有较小的刚度来产生较大的形变，以使敏感质量等惯性结构具有较大的运动幅度；同时还要考虑到悬臂梁与锚点相连的固定端处必须满足强度的要求。综合以上梁的特点，在某些特定的情况下，设计此种变截面梁结构对于MEMS器件的设计是必须的。

针对MEMS结构和器件的整体行为的快速建模与仿真要求，西北工业大学的霍鹏飞在其论文“基于组件网络方法的微加速度计建模与仿真”中，提出了基于多端口组件网络MuPEN(multi-port-element network)的MEMS系统级建模和设计方法，并建立了参数化系统级组件库。该方法把整个MEMS器件分解为多个功能结构部件，各个功能结构部件建立对应的多端口参数化系统级组件，通过这些参数化系统级组件的相互连接形成网络表述整个MEMS器件，并进行仿真分析。另外，根据相似的方法创建的组件库还有Carnegie Mellon大学的NODAS，Coventor ware^TM的Architect等。

当前，国内外MEMS设计软件的系统级参数化组件库中，梁组件均为等截面梁，都没有宽度随长度线性变化的变截面梁系统级组件，因此无法对具有此种结构的MEMS器件进行系统级仿真设计，所以MEMS系统级组件库迫切需要此类参数化的组件模型。

发明内容

为了克服上述技术问题，本发明提出一种针对宽度随长度方向线性变化的变截面梁的系统级建模方法，解决了当前对具有此种结构的MEMS器件无法进行系统级仿真设计的问题。

本发明提出的MEMS系统级设计中的一种变截面梁建模方法，包括如下步骤：

步骤一：建立变截面梁的三维局部坐标系坐标系xyz。

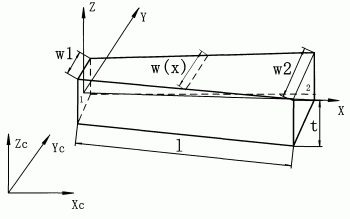
已知变截面梁弹性模量E，泊松比为υ，密度为ρ，阻尼系数为B′，以变截面梁的长度方向为x轴，宽度方向为y轴，厚度方向为z轴建立局部坐标系xyz，参阅图1。图中l为梁长度，t为厚度，w1为端面1的宽度，w2为端面2的宽度且w1≤w2，x_Cy_Cz_C为全局坐标系。

步骤二：根据结构力学得到变截面梁在xoy平面内的弯曲刚度矩阵[k_yij](i＝1，2、j＝1，2)和在xoz平面内的弯曲刚度矩阵[k_zij](i＝1，2、j＝1，2)。

将端面2约束建立悬臂梁力学模型，对于宽度随长度线性变化的变截面梁，任意截面上的宽度w(x)表达式为

w(x)=w1+(w2-w1)xl---(1)]]>

在xoy平面内，当变截面梁横截面为矩形时，梁任意截面处的转动惯量I_z(x)为

Iz(x)=(w1+(w2-w1)xl)3t12---(2)]]>

参阅图2，当梁端面1受到弯矩M_xoy1时，根据纯弯曲方程

d2ωxoydx2=Mxoy1EIz(x)---(3)]]>

式中ω_xoy为轴线上任一点在xoy平面内的挠度。结合边界条件当x＝1时，端面2处的挠角θ_xoy2＝0、挠度ω_xoy2＝0。对式(3)积分求出在端面1(x＝0)处的挠角θ_xoy1和挠度ω_xoy1表达式分别为

θxoy1=6lMxoy1Et(w1+w2)w22w12---(4)]]>

ωxoy1=-6l2Mxoy1Et1w22w1---(5)]]>

参阅图3，当梁端面1处受到集中力F_xoy1时，纯弯曲方程变为

d2ωxoydx2=xFxoy1EIz(x)---(6)]]>

同理，端面1(x＝0)处的挠角和挠度表达式分别为

θxoy1=-6l2Fxoy1Et1w22w1---(7)]]>

ωxoy1=6l3Fxoy1Et(3w22+2ln(w1)w22-4w1w2-2ln(w2)w22+w12)(w1-w2)3w22---(8)]]>

令：A1=6lEt(w1+w2)w22w12]]>

B1=-6l2Et1w22w1]]>

C1=-6l2Et1w22w1]]>

D1=6l3Et(3w22+2ln(w1)w22-4w1w2-2ln(w2)w22+w12)(w1-w2)3w22]]>

可从式(4)、(5)、(7)、(8)中解出

Fxoy1=A1(A1D1-B1C1)ωxoy1+B1(B1C1-A1D1)θxoy1---(9)]]>

Mxoy1=C1(B1C1-A1D1)ωxoy1+D1(A1D1-B1C1)θxoy1---(10)]]>

对于xoy平面内变截面梁弯曲的刚度方程

Fxoy1Mxoy1Fxoy2Mxoy2=ky11ky12ky21ky22ωxoy1θxoy1ωxoy2θxoy2---(11)]]>

式中[k_yij](i＝1，2、j＝1，2)为变截面梁在xoy平面内的弯曲刚度矩阵，因此其中

ky11=A1A1D1-B1C1B1B1C1-A1D1B1B1C1-A1D1D1A1D1-B1C1---(12)]]>

利用受力平衡可求出端面2所受反力F_xoy2＝-F_xoy1和弯矩M_xoy2＝F_xoy1l-M_xoy1，可知

ky21=-A1A1D1-B1C1-B1B1C1-A1D1A1l-B1B1C1-A1D1B1l-D1A1D1-B1C1---(13)]]>

同理，当约束端面1，在自由端端面2处分别施加弯矩M_xoy2和集中力F_xoy2，可分别解出[k_yij]中的k_y12、k_y22，其表达式为

ky22=A2A2D2-B2C2B2B2C2-A2D2B2B2C2-A2D2D2A2D2-B2C2]]>ky22=-A2A2D2-B2C2-B2B2C2-A2D2A2l-B2B2C2-A2D2B2l-D2A2D2-B2C2---(14)]]>

式中A2=6lEt(w1+w2)w22w12]]>

B2=6l2Et1w12w2]]>

C₂＝B₂

D2=6l3Et(-3w12-2ln(w2)w12+4w1w2-w22+2ln(w1)w12)(w1-w2)3w12]]>

在xoz平面内，梁任意截面处的转动惯量I_y(x)为

Iy(x)=(w1+(w2-w1)xl)t312---(15)]]>

与xoy面内弯曲同理，可求出在xoz平面内的弯曲刚度矩阵[k_zij](i＝1，2、j＝1，2)，其表达式为

kz11=A3A3D3-B3C3B3B3C3-A3D3B3B3C3-A3D3D3A3D3-B3C3]]>kz21=-A3A3D3-B3C3-B3B3C3-A3D3A3l-B3B3C3-A3D3B3l-D3A3D3-B3C3]]>

kz22=A4A4D4-B4C4B4B4C4-A4D4B4B4C4-A4D4D4A4D4-B4C4]]>kz12=-A4A4D4-B4C4-B4B4C4-A4D4A4l-B4B4C4-A4D4B4l-D4A4D4-B4C4---(16)]]>

式中A3=12lEt3ln(w1/w2)w1-w2]]>

B3=12l2Et3w1ln(w1)-w1+w2-w1ln(w2)(w1-w2)2]]>

C₃＝B₃

D3=6l3Et3-3w12-2w12ln(w2)+4w1w2-w22+2w12ln(w1)(w1-w2)3]]>

A4=12lEt3ln(w1/w2)w1-w2]]>

B4=-12l2Et3w1-w2+w2ln(w2)-w2ln(w1)(w1-w2)2]]>

C₄＝B₄

D4=6l3Et33w22+2w22ln(w1)-4w1w2-2w22ln(w2)+w12(w1-w2)3]]>

步骤三：计算变截面梁的轴向拉压刚度系数k_x1、k_x2和扭转刚度系数k_t1、k_t2。

参阅图4，建立变截面悬臂梁模型，当变截面悬臂梁端面2约束、端面1受到轴向力F_N和扭矩T作用时，变截面梁的轴向位移Δl和扭角 的表达式分别为

Δl=∫0lFNdxEw(x)t---(17)]]>

将(1)代入(17)、(18)，并令

kx1=1∫0ldxEw(x)t---(19)]]>

kt1=1∫0l72G[1tw3(x)+1t3w(x)]dx---(20)]]>

其中，G＝E/(2+υ)为剪切模量。则k_x1、k_t1分别为端面1的轴向拉压刚度系数和扭转刚度系数。

由受力平衡可知，端面2的轴向拉压刚度系数、扭转刚度系数分别为k_x2、k_t2，即k_x2＝-k_x1、k_t2＝-k_t1。

步骤四：将上述推导出的弯曲刚度矩阵[k_yij]、[k_zij](i＝1，2、j＝1，2)、轴向拉压刚度系数k_x1、k_x2和扭转刚度系数k_t1、k_t2按照矩阵方式表出，最终得出在局部坐标系下维数为12×12的变截面梁刚度矩阵K，其具体表达式为

K=kx100000kx2000000ky11(1,1)000ky11(1.2)0ky12(1,1)000ky12(1,2)00kz11(1,1)0kz11(1,2)000kz12(1,1)0kz12(1,2)0000kt100000kt20000kz11 MEMS系统级设计中的一种变截面梁建模方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。