专利摘要

本发明请求保护一种贝塞尔函数与Toeplitz算法相结合的方法，属于信号处理技术领域。该方法通过贝塞尔函数性质及雅可比变换处理SFM信号，然后结合阵列信号处理算法检测和估计SFM信号的参数。该方法解决了SFM信号变换后的信号协方差矩阵不接近真实值的问题。该方法不仅能够准确的、较全面的估计出该信号的各个参数，且可以估计出多分量的SFM信号参数。

权利要求

1.一种SFM信号的参数估计方法，其特征在于，采用贝塞尔函数处理SFM信号，获得窄带正弦信号，根据窄带正弦信号建立接收信号的协方差矩阵 通过Toeplitz算法对协方差矩阵 进行预处理，获得重构信号的协方差矩阵R_T，对协方差矩阵R_T进行特征值分解，得到数据的信号子空间和噪声子空间，从而求得谐波角频率，获得载波频率和调制频率估计，根据第一类贝塞尔函数的递归关系J_v+1(m_f)＝2vJ_v(m_f)/m_f-J_v-1(m_f)，估计调制系数及谐波幅度。

2.根据权利要求1所述的方法，其特征在于，所述贝塞尔函数处理SFM信号具体为：将SFM信号分解成一组具有谐波幅度谐波频率的窄带正弦信号和的形式，其谐波幅度为：C＝[AJ_-V(m_f) L AJ₀(m_f) L AJ_V(m_f)]，各个谐波频率为：f₁＝f_c-Vf_m,L,f_V+1＝f_c+0f_m,L,f_2V+1＝f_c+Vf_m，其中，A为信号的幅度，f_c为信号载波频率，f_m为信号调制频率，m_f为调频系数，J_v(k)是第一类v阶贝塞尔函数，v＝1，……，V为第一类贝塞尔函数阶数。

3.根据权利要求1所述的方法，其特征在于，通过Toeplitz预处理具体为：调用公式： 使得矩阵接近真实的数据协方差矩阵R，对数据协方差矩阵的斜对角线上的元素进行平均，其中，S_T是Toeplitz矩阵集。

4.根据权利要求1所述的方法，其特征在于，调用公式 0≤n＜M对阵列的数据协方差矩阵 进行求值运算，得到一个新的矢量$\hat{r}=({\hat{r}}_T(-(M-1)),···,{\hat{r}}_T(-1),{\hat{r}}_T\left(0\right),{\hat{r}}_T\left(1\right),···,{\hat{r}}_T(M-1)),$通过该矢量重构数据协方差矩阵R_T，其中，M为阵元数， 为 中的元素， 为 斜对角线上元素的平均。

5.根据权利要求1所述的方法，其特征在于，对协方差矩阵R_T进行特征值分解具体为，对R_T进行特征值分解，得到由大特征值及小特征值组成的对角阵D＝diag[λ₁ λ₂ L λ_M],其中，特征值满足关系：

λ₁≥λ₂≥L≥λ_Q＞λ_Q+1＝L＝λ_M＝σ²，根据公式R_n＝σ²I求得噪声功率，调用公式：R_T＝BR_sB^H+R_n求得其信号协方差矩阵R_s，取其实部开方即得其谐波幅度。

6.根据权利要求1所述的方法，其特征在于，所述获得窄带正弦信号具体包括：对给定的SFM信号s(t)，在t＝nΔt时刻对其进行离散化，得到离散采样序列为{s(n)}；调用公式：$\exp \left(\mathrm{jk}\sin \beta \right)=\underset{v=-\infty }{\overset{\infty }{\Sigma }}{J}_v\left(k\right)\exp \left(\mathrm{jv\beta }\right)$对离散化后的信号进行变换，得到无穷多项具有谐波幅度谐波频率的正弦信号之和，根据公式：J_v(m_f)＝(-1)^vJ_-v(m_f)得到一组具有谐波幅度谐波频率的窄带正弦信号。

7.根据权利要求1所述的方法，其特征在于，所述调制系数的估计具体包括，根据贝塞尔函数的递归关系：J_v+1(m_f)＝2vJ_v(m_f)/m_f-J_v-1(m_f)，从第一类贝塞尔函数的最高阶数依次往下，建立所有的递推关系式组成超定方程组，计算方程组的最小二乘解，即为调制系数

说明书

技术领域

本发明涉及信号处理技术，尤其涉及复正弦调频（SFM）信号参数估计方法。

背景技术

复正弦调频（SFM）信号是非平稳信号中的一种，它的瞬时频率是一个随着时间非线性变化的正弦函数。相位函数的非线性导致了信号的非平稳性，所以复正弦调频（SFM）信号的频率随时间有较大的变化，且呈现较强的时间局部特性。传统时域和频域的分析法都不能象分析平稳信号那样适用了，因此需要有效的研究方法来处理此类信号。

时频分析是处理非平稳信号的有效手段，最常用的方法是将Wigner-Ville分布（WVD）与阵列信号处理相结合，但在多信号的情况下WVD计算相当复杂，对采样率要求很高，而且容易受到交叉项的干扰，这些都降低了此类方法的实用性。为此，李立萍等人（李立萍，黄克骥等.基于STFT的相干宽带调频信号2-D到达角估计[J].电子与信息学报,2005.27（11）：1760-1764.）采用短时傅里叶变换（STFT）建立空间时频分布，避免了WVD交叉项的干扰，计算简单。但是该方法在计算空间时频分布时对窗口长度进行了限制，以满足信号瞬时频率近似不变的假设。Peleg等（PELEGS,FRIEDLANDERB.The discrete poly-nomial-phase transform[J].IEEE Trans.on Signal Processing,1995,43（8）:1901-1904.）利用离散多项式相位变换实现正弦调频信号的波形重构，但没有提供参数估计算法。吕远等人（吕远，祝俊，唐斌.基于DPT的非线性调频信号参数估计[J].电子测量与仪器学报,2009,23（6）:63-67.）通过离散多项式变换实现复正弦调频信号的参数估计，但深度调制情况下算法性能较差。

综上所述，对复正弦调频信号的参数估计方法研究较少，或受参数限制或只能估计部分参数，因此，目前还没有普遍适用复正弦调频信号的处理算法。

发明内容

本发明所要解决的技术问题是，在对复正弦调频（SFM）信号参数估计过程中，复正弦调频（SFM）信号存在非平稳性及分解后的协方差矩阵不接近真实值的问题。提出贝塞尔函数与托普利兹（Toeplitz）算法相结合的SFM信号参数估计方法，在信号处理过程中，可以有效地对SFM信号进行分解，即把其分解成一组具有谐波幅度谐波频率的窄带正弦信号和的形式。从而结合Toeplitz算法重构协方差矩阵，然后利用信号子空间的方法估计SFM的参数。该方法不仅测频精度高，而且估计性能好。

本发明解决上述技术问题的技术方案是，一种SFM信号的参数估计方法，一种SFM信号的参数估计方法，其特征在于，采用贝塞尔函数处理SFM信号，获得窄带正弦信号，根据窄带正弦信号建立接收信号的协方差矩阵 通过Toeplitz算法对协方差矩阵 进行预处理，获得重构信号的协方差矩阵R_T，对协方差矩阵R_T进行特征值分解，得到数据的信号子空间和噪声子空间，利用MUSIC算法求得谐波角频率，从而获得载波频率和调制频率估计，再根据第一类贝塞尔函数的递归关系J_v+1(m_f)＝2vJ_v(m_f)/m_f-J_v-1(m_f)，估计调制系数及谐波幅度。

所述贝塞尔函数处理SFM信号具体为：将SFM信号分解成一组具有谐波幅度谐波频率的窄带正弦信号和的形式，其谐波幅度为： 各个谐波频率为：f₁＝f_c-Vf_m,L,f_V+1＝f_c+0f_m,L,f_2V+1＝f_c+Vf_m，其中，A为信号的幅度，f_c为信号载波频率，f_m为信号调制频率，m_f为调频系数，J_v(k)是第一类v阶贝塞尔函数，v＝1，……，V为第一类贝塞尔函数阶数。

通过Toeplitz预处理具体为：调用公式： 使得矩阵接近真实的数据协方差矩阵R，对数据协方差矩阵的斜对角线上的元素进行平均，其中，S_T是Toeplitz矩阵集。

调用公式 0≤n＜M对阵列的数据协方差矩阵 进行求值运算，得到一个新的矢量r^=(r^T(-(M-1)),···,r^T(-1),r^T(0),r^T(1),···,r^T(M-1)),]]>通过该矢量重构数据协方差矩阵R_T，其中，M为阵元数， 为 中的元素， 为 斜对角线上元素的平均。对协方差矩阵R_T进行特征值分解具体为，对R_T进行特征值分解，得到由大特征值及小特征值组成的对角阵D＝diag[λ₁ λ₂ L λ_M],其中，特征值满足关系：λ₁≥λ₂≥L≥λ_Q＞λ_Q+1＝L＝λ_M＝σ²，根据公式R_n＝σ²I求得噪声功率，调用公式：R_T＝BR_sB^H+R_n求得其信号协方差矩阵R_s，取其实部开方即得其谐波幅度。所述获得窄带正弦信号具体包括：对给定的SFM信号s(t)，在t＝nΔt时刻对其进行离散化，得到离散采样序列为{s(n)}；调用公式：exp(jksinβ)=Σ∞Jv(k)exp(jvβ)]]>对离散化后的信号进行变换，得到无穷多项具有谐波幅度谐波频率的正弦信号之和，根据公式：J_v(m_f)＝(-1)^vJ_-v(m_f)得到一组具有谐波幅度谐波频率的窄带正弦信号。根据贝塞尔函数的递归关系：J_v+1(m_f)＝2vJ_v(m_f)/m_f-J_v-1(m_f)，从第一类贝塞尔函数的最高阶数依次往下，建立所有的递推关系式组成超定方程组，计算方程组的最小二乘解，即为调制系数

本发明在贝塞尔函数处理SFM信号的基础上，采用阵列信号处理的方法（Toeplitz算法、MUSIC算法）来检测和估计SFM信号的参数。该方法不仅能够很好的处理SFM信号，而且频率估计效果非常好，且不受参数限制，计算量小，能够较全面的估计SFM信号的参数。

附图说明

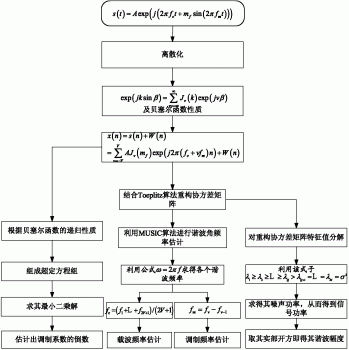
图1本发明SFM信号参数估计流程图；

图2SFM信号的时域波形图；

图3SFM信号的频域波形图；

图4SFM信号瞬时频率与时间的变化关系；

图5m_f＝1时的谐波幅度；

图6m_f＝2时的谐波幅度；

图7本发明变换后的窄带信号实部；

图8变换后各个谐波分量的谱线图；

图9本发明贝塞尔函数与Toeplitz算法相结合的各个谐波角频率估计。

具体实施方式

本发明在贝塞尔函数处理SFM信号的基础上把分解后的窄带正弦信号按照波达方向估计的方法进行频率检测和估计，解决了SFM信号不好处理及受其他参数估计限制的问题。

以下直接采用公式推导的方法，推导出复正弦调频信号的载波频率f_c、调制频率f_m、调制系数m_f及谐波幅度参数。

SFM信号的参数估计具体为，复正弦调频信号表示为：

s(t)＝Aexp(j(2πf_ct+m_fsin(2πf_mt))),0≤t≤T

                                                 （1）

其中，A为信号的幅度，f_c为信号载波频率，f_m为信号调制频率，m_f为调频系数。在t＝nΔt时刻对给定信号s(t)离散化得到离散采样序列为{s(n)}：

s(n)＝Aexp(j(2πf_c(nΔt)+m_fsin(2πf_m(nΔt)))),0≤n≤N-1

                                                （2）

其中，N为采样长度，Vt为采样间隔。

接收信号可表示为：

x(n)＝s(n)+W(n)

＝Aexp(j(2πf_c(nΔt)+m_fsin(2πf_m(nΔt))))+W(nΔt),0≤n≤N-1

                                                   （3）

其中，W为零均值的高斯白噪声。

对离散化后的信号根据雅可比展开恒等式：

exp(jksinβ)=Σv=-∞∞Jv(k)exp(jvβ)---(4)]]>

其中，J_v(k)是第一类v阶贝塞尔函数。把式（4）代入式（3）可得无穷多个具有谐波幅度谐波频率的正弦信号之和的形式，一般情况下可取Vt＝1，即：

x(n)=s(n)+W(n)]]>

=Aexp(j(2πfcn+mfsin(2πfmn)))+W(n)]]>

=Σv=-∞∞AJv(mf)exp(j2π(fc+vfm)n)+W(n),0≤n≤N-1---(5)]]>

由式（5）可以看出，非线性的复正弦调频信号被变成了无穷多项线性的正弦信号和的形式。其中， 由贝塞尔函数的对称性质：J_v(m_f)＝(-1)^vJ_-v(m_f)，并且当|v|＞|V|时，J_v(m_f)≈0，s(n)部分分量小到可以被忽略不计。故式（5）可以写成：

x(n)≈Σv=-VVAJv(mf)exp(j2π(fc+vfm)n)+W(n),0≤n≤N-1]]>

=AJ-V(mf)exp(j2π(fc-Vfm)n)+L+AJ0(mf)exp(j2π(fc+0fm)n)]]>

+L+AJV(mf)exp(j2π(fc+Vfm)n)+W(n)---(6)]]>

其中，V是信号分量不可以被忽略的第一类贝塞尔函数的最高阶数。即当m_f＞1时，V≈m_f+1，然而当m_f∈[0.14,1]时，V＝1或2；当m_f∈[0，0.14)时，V＝0。

由式（6）可以看出，经过贝塞尔函数分解后，SFM信号被分解成了一组具有谐波幅度谐波频率的窄带正弦信号和的形式，其谐波幅度为： 各个谐波频率为：f₁＝f_c-Vf_m,L,f_V+1＝f_c+0f_m,L,f_2V+1＝f_c+Vf_m。这就是贝塞尔函数分解SFM信号的过程，该方法能够很好的把SFM信号处理成能够用常规算法来估计的窄带信号形式。

由式（6）知，SFM信号经过贝塞尔函数性质及雅可比变换被变换成了一组窄带正弦信号和的形式。然后根据其窄带信号模型求出其真实的数据自协方差矩阵R。在理想情况下，阵列接收数据的协方差矩阵 具有Toeplitz性质，而实际情况中，由于受误差的影响，阵列接收数据的协方差矩阵 一般只是对角占优的矩阵。故在此通过Toeplitz预处理使得矩阵接近真实的数据协方差矩阵R。

即

minRT∈ST|RT-R|---(7)]]>

这里S_T是Toeplitz矩阵集。Toeplitz算法就是对数据协方差矩阵的斜对角线上的元素进行平均。可以用以下两式进行等价，即：

r^T(-n)=1M-nΣi=1M-nr^i(i+n),0≤n<M---(8)]]>

r^T(n)=r^T*(-n)---(9)]]>

其中，M为阵元数， 为 中的元素， 为 斜对角线上元素的平均。

利用式(8)对阵列的数据协方差矩阵 进行求值运算，得到一个新的矢量r^=(r^T(-(M-1)),···,r^T(-1),r^T(0),r^T(1),···,r^T(M-1)),]]>通过该矢量重构数据协方差矩阵R_T，从而对R_T特征值分解，得到信号子空间和噪声子空间，然后利用MUSIC算法进行谐波角频率的估计，从而估计出其载波频率和调制频率。

以上是信号的载波频率、调制频率的估计。

为了解决受参数限制或者只能估计部分参数的问题，本发明还给出了调制系数及谐波幅度估计。

由第一类贝塞尔函数，可以得到以下递归关系：

J_v+1(m_f)＝2vJ_v(m_f)/m_f-J_v-1(m_f)       （10）

由式（10）的递归关系我们做如下推导，假设贝塞尔函数分解的最高阶数为V，则贝塞尔函数的各个阶数分别为-V -V+1 L V。则有下列式成立：

而式（11）又可以分解成如下形式：

J=JV(mf)JV-2(mf)MJ-V+2(mf)=2(V-1)JV-1(mf)-JV-2(mf)2(V-2)JV-2(mf)-JV-3(mf)MMMM2(-V+1)J-V+1(mf)-J-V(mf)·1mf1=Zb---(12)]]>

根据超定方程组的定义可知，式（12）是超定方程组，所谓超定方程组是指方程个数大于未知量个数的方程组。

当Z^TZ可逆时，超定方程组（12）存在最小二乘解，且即为方程组Z^TZb＝Z^TJ的解，即b＝(Z^TZ)^-1Z^TJ。于是有：1/mf1=(ZTZ)-1ZTJ.]]>从而可以计算出调制系数，最小二乘解为调制系数。

对重构得到的数据协方差矩阵R_T进行特征值分解，从而得到由大特征值及小特征值组成的对角阵D＝diag[λ₁ λ₂ L λ_M],而上式中的特征值满足以下关系：λ₁≥λ₂≥L≥λ_Q＞λ_Q+1＝L＝λ_M＝σ²，从而求得噪声功率R_n＝σ²I；利用公式：R_T＝E[XX]＝BR_sB^H+R_n，求得其信号协方差矩阵R_s，取其实部开方即得其谐波幅度。

下面结合具体的附图及仿真实例，对本发明的实施作更进一步的详细说明，但本发明的实施方式并不仅限于此。

如图1所示为本发明贝塞尔函数和Toeplitz算法相结合的参数估计方法流程图，对SFM信号参数估计具体步骤如下，假设有两个相同时频分布的宽带SFM信号：

s₁(t)＝A₁exp{j[2π*f_ct+m_f*sin(2π*f_mt)]}

s₂(t)＝A₂exp{j[2π*f_ct+m_f*sin(2π*f_mt)]}

信号参数设置为：m_f＝1，f_c＝0.35，f_m＝0.03，信号幅度为A₁＝1，A₂＝2A₁，SNR＝20dB，快拍数N＝256。

步骤1：在t＝nΔt时刻对给定信号s₁(t)、s₂(t)离散化得到离散采样序列为{s₁(n),s₂(n)}。

步骤2：利用雅可比展开式：exp(jksinβ)=Σv=-∞∞Jv(k)exp(jvβ),]]>并根据贝塞尔函数的对称性质可得变换后窄带信号x(n)可以表示为：

x(n)≈Σv=-22AJv(mf)exp(j2π(fc+vfm)n)+W(n),0≤n≤N-1---(13)]]>

经过分解，式（13）可以写成下面的表达形式:

x(n)≈Σv=-22AJv(mf)exp(j2π(fc+vfm)n)+W(n),0≤n≤N-1]]>

=AJ-2(mf)exp(j2π(fc-2fm)n)+AJ-1(mf)exp(j2π(fc-1fm)n)]]>

+AJ0(mf)exp(j2π(fc+0fm)n)+AJ1(mf)exp(j2π(fc+1fm)n)]]>

+AJ2(mf)exp(j2π(fc+2fm)n)+W(n)---(14)]]>

步骤3：由式（14）求得阵列模型接收的数据协方差矩阵，采用Toeplitz算法对其进行预处理，得到重构的数据协方差矩阵。

步骤4：对重构的数据协方差矩阵特征值分解，从而得到信号子空间和噪声子空间以及其特征值空间。

步骤5：利用MUSIC算法的谱估计公式求得各个谐波角频率。

步骤6：根据贝塞尔函数的对称性及估计出的各个谐波角频率从而估计出载波频率和调制频率。

步骤7：由式（10）、式（11）可知，当m_f＝1时，即第一类贝塞尔函数的最高阶数为2时，该递归关系可以表示为：

v=1,J2(mf)=2J1(mf)/mf-J0(mf)v=0,J1(mf)=2g0gJ0(mf)/mf-J-1(mf)v=-1,J0(mf)=2g(-1)gJ-1(mf)/mf-J-2(mf)---(15)]]>

于是由式（15）可以得到如下关系：

J=2J1(mf)-J0(mf)2g0gJ0(mf)-J-1(mf)2g(-1)gJ-1(mf)-J-2(mf)g1mf1=JZ1mf1---(16)]]>

故由1/mf1=(JZTJZ)-1JZTJ]]>J从而估计出调制系数

步骤8：根据小特征值和噪声功率相等的特点，从而求得其噪声功率为R_n＝σ²I＝小特征值，然后利用公式：R_T-R_n＝BR_sB^H，求得其信号协方差矩阵R_s，取其实部开方即得谐波幅度。

为了更好的了解SFM信号的非平稳特性，下面分别从时域、频域、时频域来分析该信号，其波形图分别见图2、图3、图4所示。

由式(1)所示的复正弦调频信号的时域表达式，可得其瞬时频率表达式为：

fSFM(t)=fc+mfωm2πcos(ωmt)---(17)]]>

信号的时域波形如图2所示，从图中可以看出该信号是一个复杂的信号，并且可以看出其持续时间及信号幅度随时间的变化关系；从频域看即图3，我们仅仅知道它的频率成分，却看不到其时间信息；然而信号的瞬时频率如图4所示，不仅能看出信号时间与频率的信息，而且能表示出信号的频率与时间的变化关系，给出了一个二维的时间-频率的直观描述。

图5、图6是本发明不同调制频率的谐波幅度图，该组图证明了第一类贝塞尔函数的对称性质以及v≈m_f+1，当|v|＞|m_f|时，J_v(m_f)≈0，即s(n)部分分量小到可以被忽略不计。图5取m_f＝1，当V≥3时，可以明显看出J₃(1)≈0；图6取m_f＝2，当V≥4时，可以明显看出J₄(2)≈0。

由式(6)、(14)可知，被贝塞尔函数及雅可比变换信号变成了一组窄带正弦信号。其仿真结果如图7、图8所示。图7给出了变换后的窄带信号分别在没有噪声和SNR=20dB时，信号的实部幅值特性图。从图中可以看出经过变换后，当没有噪声时，信号变换成了窄带的信号；当SNR=20dB时，接收的信号变换成了窄带信号和噪声。从而把宽带的信号变成了窄带的信号，有利于用比较成熟的方法进行参数估计。图8给出了变换后各个谐波分量的谱线图。即与图5中的各个非零部分的谐波频率相对应。

由以上分析可知，SFM信号经过贝塞尔函数变换后，结合Toeplitz算法重构数据协方差矩阵，从而采用MUSIC算法进行参数估计。其仿真结果如图9所示，在前面的信号参数已知的情况下，各个谐波频率的理论值应该为：

f₁＝(f_c-2f_m)＝0.29,f₂＝(f_c-1f_m)＝0.32,f₃＝(f_c+0f_m)＝0.35。则这5个谱f₄＝(f_c+1f_m)＝0.38,f₅＝(f_c+2f_m)＝0.41

峰分别对应的谐波角频率理论值为：

ω₁＝2πf₁＝(f_c-2f_m)*2π＝0.58π,ω₂＝2πf₂＝(f_c-f_m)*2π＝0.64π

ω₃＝2πf₃＝(f_c)*2π＝0.7π,ω₄＝2πf₄＝(f_c+f_m)*2π＝0.76π

ω₅＝2πf₅＝(f_c+2f_m)*2π＝0.82π

通过图9及以上的数据对比，很明显与Toeplitz算法相结合的频率估计方法能够很好的估计出各个谐波角频率，从而利用公式ω＝2πf估计出各个谐波频率，然后再根据这些谐波频率的对称性，即所有谐波频率之和是载波频率的整数倍，得

基于贝塞尔函数与Toeplitz算法的SFM信号参数估计方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。