专利摘要
本发明提供一种控制多枚导弹攻击角度和攻击时间的方法,其可准确地控制多枚导弹对目标的攻击时间和攻击角度;该方法为:从多枚导弹中任意选取一枚为领弹,以目标为球心、领弹与目标之间的距离为半径构造虚拟球体;将剩余的导弹定义为从弹,在虚拟球体表面为每一从弹选定虚拟点,其中每一虚拟点与目标之间连线的方向为其对应从弹的预设的理想攻击角度;通过控制从弹运动轨迹逼近并跟踪虚拟点轨迹,从而实现对多枚导弹攻击角度和攻击时间的控制。本发明的控制导弹攻击角度和攻击时间的方法,其通过利用从弹对其对应的虚拟点的逼近并跟踪来实现,因此无需事先对每一从弹指定理想的攻击时间,便可对从弹的攻击角度和攻击时间进行控制。
说明书
技术领域
本发明涉及一种控制多枚导弹攻击角度和攻击时间的方法,属于制导技术领域。
背景技术
随着科学技术的高速发展,导弹防御系统的能力不断增强,单枚导弹作战在很多情况下已无法满足战场的要求,多枚导弹协同作战变得越来越重要。为了提高导弹协同作战的杀伤力,通常对攻击角度有要求,而为了实现饱和攻击,又对攻击时间有要求。如果多枚导弹能够从不同的角度同时攻击目标,将大大增强导弹的打击能力。
国内外关于对导弹攻击角度和攻击时间同时进行控制的技术还处于初级阶段。目前,国内外对于具有攻击角度约束的制导控制方法的研究开展得比较多,此方面的制导控制方法主要分为两类:基于最优控制理论的方法和基于比例导引律的方法。对具有攻击时间约束的导弹制导控制方法的研究相对来说比较少,而同时考虑对攻击角度和攻击时间进行控制的方法就更少。在先技术[1](参见Lee J I,Jeon I S,Tahk M J.Guidance law to control impact time and angle.IEEE Transactions on Aerospace and Electronic Systems,2007,43(1):301-310)中,基于最优控制理论提出了可同时控制多枚导弹攻击方位角和攻击时间的制导方法,但它只适用于导弹在二维平面攻击目标的情况。在先技术[2](参见Jeon I S,Lee J I,Tahk M J.Guidance law to controlimpact time and angle.International Conference on Control and Automation.Hungary:Budapest,2005:852-857)中,基于传统的比例导引律设计了一种具有攻击角度和时间约束的、适用于反舰导弹的制导方法,但本方法只适用于攻击固定目标,而且并没有对制导方法参数的取值进行说明。在先技术[3](参见张友安,马培蓓.带有攻击角度和攻击时间控制的三维制导,航空学报,2008,29(4):1020-1026)中,先基于李雅普诺夫稳定性理论设计了带有攻击角度控制的三维制导律,采用此制导律将导弹导引到预定的攻击角度上,然后通过圆弧机动飞行来对攻击时间进行控制,但此技术中需要预先设定理想攻击时间,而理想攻击时间的合理设定一直是一个难点。
发明内容
本发明要解决的技术问题是克服上述已有技术的困难,在不需要事先指定理想攻击时间以及不限定目标运动状态的前提下,提供一种控制多枚导弹攻击角度和攻击时间的方法。
实现本发明的技术方案如下:
一种控制多枚导弹攻击角度和攻击时间的方法,具体步骤为:
步骤一、在协同作战的多枚导弹中,任意选取一枚作为领弹,并根据武器系统的总体作战要求,为领弹选取任一制导律;同时以目标为球心,以领弹与目标之间的距离为半径构造虚拟球体;
步骤二、将剩余的导弹定义为从弹,根据导弹协同作战的需求,参考领弹对目标的攻击情况,为每一从弹设定理想攻击角度,该攻击角度都是以地面坐标系为基准设定的;同时在虚拟球体表面为每一从弹选定虚拟点,每一虚拟点与目标之间连线的方向为其对应从弹的理想攻击角度,其中虚拟点的位置随着领弹与目标的逼近不断更新;
步骤三、通过控制从弹运动轨迹跟踪并逼近虚拟点轨迹,从而实现对多枚导弹攻击角度和攻击时间的控制。
进一步地,本发明步骤三的过程为:
步骤101、在地面坐标系中,建立目标的运动模型、从弹的运动模型及虚拟点位置模型,根据所建立的模型在地面坐标系中建立从弹与虚拟点之间的相对运动模型;该步骤的具体过程为:
步骤I、在地面坐标系中建立目标的运动模型:
其中XT=[xT,yT,zT]表示目标的位置,VT为目标的速度,θT和ψVT为目标速度矢量与地面坐标系坐标轴的夹角;
步骤II、由于虚拟点与目标之间的距离等于领弹与目标之间的距离,虚拟点的运动方向为设定的从弹理想攻击角,因此,在地面坐标系中建立表征虚拟点位置模型为:
其中:Xv=[xv,yv,zv]为虚拟点的坐标,rl为领弹与目标之间的距离,εy、εz分别为从弹在俯仰方向和偏航方向设定的理想攻击角;
步骤III、在地面坐标系中建立从弹的运动模型为:
其中:Xm=[xm,ym,zm]表示从弹的位置,V为从弹的速度,θ和ψV为从弹的弹道倾角和弹道偏角;
步骤IV、根据步骤I-III所建立的模型,在地面坐标系中建立从弹与虚拟点之间的相对运动模型;
从弹和虚拟点之间的相对位置为:
对式(4)求导可得到从弹与虚拟点的相对速度差:
将式(5)写为向量形式为:
其中:Xd=[xd yd zd]T,T4=[-cosεycosεz -sinεy cosεysinεz]T, 领弹与目标之间的距离的变化率;
步骤102、建立描述从弹运动的质心动力学方程、姿态运动学方程以及姿态动力学方程,结合以上推导的从弹与虚拟点的相对运动模型,得到对从弹攻击角度和攻击时间进行控制的非线性控制模型,基于反馈线性化理论对所述非线性控制模型进行精确线性化,获取线性的控制模型;
步骤103、将线性化后的控制模型看作一个终端时间无限的状态调节器,采用线性二次型性能指标,基于最优控制理论设计从弹控制器,使控制器输出为零,利用该设计的从弹控制器实现对虚拟点的跟踪和逼近,从而实现对从弹攻击角度和攻击时间的控制。
进一步地,本发明当领弹按照指定的制导律飞向目标时,虚拟点轨迹为一条直线,为了降低对从弹可用过载和控制能量的要求,按照设定的时间步长对虚拟点位置模型进行改进设计,在地面坐标系中更新虚拟点虚拟点位置模型为:
其中:rf为从弹与目标之间的距离,εyf、εzf分别为从弹在俯仰方向和偏航方向的实际视线角,N为整数且其取值方法为:
其中:tgo为预估的领弹飞行时间,h为设定的时间步长;
其中:n为取遍[1,2,…,N]的整数,当领弹飞过一个时间步长时,n取1,当领弹飞过两个时间步长时,n取2,并依次类推,直至领弹飞过N个时间步长,n取N为止。
有益效果
本发明在控制攻击时间方面:由于每一虚拟点与领弹处于同于虚拟球上,虚拟点跟随领弹一步步接近目标,利用从弹对其所对应的虚拟点的跟踪与逼近,因此在无需事先对每一从弹指定理想攻击时间的情况下,实现对目标攻击时间的控制,其可适用于攻击固定或不同运动状态的目标;在控制攻击角度方面:由于每一虚拟点与目标之间连线的方向为其对应从弹的理想攻击角度,在从弹跟踪与逼近虚拟点的过程中,其相对于目标的攻击角度也逐步逼近理想攻击角度,从而实现对目标攻击角度的控制;本发明基于虚拟点的方法能够实现对从弹攻击角度和攻击时间的有效控制,从而使从弹和领弹从预设的角度同时攻击目标,达到良好的协同作战效果。本发明可应用于各种类型的导弹,具有很大的应用灵活性和广阔的军事应用前景。
其次、本发明通过对虚拟点轨迹进行改进,其可满足降低从弹的过载要求。
附图说明
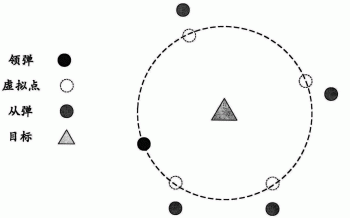
图1为本发明的总体示意图;
图2为三枚导弹协同攻击目标弹道图;
图3为两枚从弹攻击角度随时间变化图;
图4为两枚从弹推力随时间变化图;
图5为两枚从弹舵偏角随时间变化图;
图6为从弹1切向过载和法向过载随时间变化图;
图7为从弹2切向过载和法向过载随时间变化图。
具体实施方式
下面结合附图和具体实施例对本发明进行详细说明。
当前,在多枚导弹协同作战研究领域中,如何控制各导弹的攻击时间和攻击角度,来提高对目标的打击力为当前所面临的主要问题。在本发明中:
如图1所示,从多枚导弹中任意选取一枚为领弹,以目标为球心、领弹与目标之间的距离为半径构造虚拟球体;将剩余的导弹定义为从弹,在虚拟球体表面为每一从弹选定虚拟点,其中每一虚拟点与目标之间连线的方向为其对应从弹的预设的理想攻击角度;通过控制从弹运动轨迹跟踪并逼近虚拟点轨迹,从而实现对多枚导弹攻击角度和攻击时间的控制。
本发明随着领弹与目标的逼近使得虚拟球体的半径逐步缩小,通过控制从弹运动轨迹对虚拟点的跟踪与逼近,从而达到对从弹攻击时间进行控制的目的;同时由于各虚拟点与目标之间连线的方向为其对应从弹的预设的理想攻击角度,在从弹的跟踪与逼近的过程中可以保证对从弹攻击角度的控制目的;因此本发明采用构造虚拟点的方法,其很好的实现对从弹攻击角度和攻击时间的控制。
对使用符号的注释:本发明中凡是出现符号上面带“·”的表达式,其采用课本上的表达式,即为对该符号的求导,例如下文中 为对xm对时间的求导;凡是出现符号上带有“··”的表达式,其也采用课本上的表达式,即对该符号进行两次求导,例如下文出现的 ,其表示对rl对时间进行两次求导。
本发明控制多枚导弹攻击角度和攻击时间的方法,具体的过程为:
步骤一、在协同作战的多枚导弹中,任意选取一枚作为领弹,并根据武器系统的总体作战要求,为领弹选取任一制导律;如果强调领弹对目标的命中精度和领弹弹道的收敛性,则可选用比例导引律;如果强调领弹的攻击角度和对目标的毁伤效果,可选用具有角度约束的制导律;由于本发明并未对领弹采用的制导律有限制,因此,领弹可根据需要选用任一制导律。同时以目标为球心,以领弹与目标之间的距离为半径构造虚拟球体。
步骤二、将剩余的导弹定义从弹,根据导弹协同作战的需求,参考领弹对目标的攻击情况,为每一从弹设定理想的攻击角度εyi和εzi,从而实现领弹和从弹从不同的方向同时命中目标,对目标进行有效打击;其中εyi和εzi分别为从弹在俯仰方向和偏航方向设定的理想攻击角(为了描述方便,以下省去表示从弹序号的i);同时,在虚拟球体表面为每一从弹选定虚拟点,其中每一虚拟点与目标之间连线的方向为其对应从弹的预设的理想攻击角度;该攻击角度都是以地面坐标系为基准设定的。
本发明设定从弹理想的攻击角度的具体过程为:根据目标的运动情况、领弹的初始状态、领弹采取的导引律等信息先估算出领弹的攻击角度(如领弹采用带有攻击角度约束的制导律,则可直接得知领弹的攻击角度),再根据导弹协同作战的需求,为每一从弹设定理想的攻击角度。例如:估算出的领弹的攻击角为(-2°,-25°)(括号内第一项指俯仰方向攻击角,第二项指偏航方向攻击角),为了实现对目标的立体多方向攻击,可设从弹的攻击角为(-5°,-75°)、(-10°,25°)、(-15°,75°)等。
步骤三、通过控制从弹运动轨迹跟踪并逼近虚拟点轨迹,从而实现对多枚导弹攻击角度和攻击时间的控制。
下面对步骤三的具体过程进行详细说明:
在地面坐标系中,建立目标的运动模型、从弹的运动模型及虚拟点位置模型,根据所建立的模型在地面坐标系中建立从弹与虚拟点之间的相对运动模型;该步骤的具体过程为:
步骤I、在地面坐标系中建立目标的运动模型:
其中:XT=[xT,yT,zT]表示目标的位置,VT为目标的速度,θT和ψVT为目标速度矢量与地面坐标系坐标轴的夹角。
步骤II、由于虚拟点与目标之间的距离等于领弹与目标之间的距离,虚拟点的运动方向为设定的从弹理想攻击角,因此,在地面坐标系中建立表征虚拟点位置模型为:
其中:Xv=[xv,yv,zv]为虚拟点的坐标,rl为领弹与目标之间的距离,εy、εz分别为从弹在俯仰方向和偏航方向设定的理想攻击角。
本步骤中,当领弹按照指定的制导律飞向目标时,虚拟点轨迹为一条直线,当基于控制器对从弹进行控制,使其逼近和跟踪此虚拟点轨迹时,要求从弹具有较大的过载和控制能量。为了降低对从弹可用过载和控制能量的要求,对虚拟点轨迹进行改进设计,改进后的虚拟点轨迹为:
其中:rf为从弹与目标之间的距离,εyf、εzf分别为从弹的实际攻击角,N为整数且其取值方法为:
其中:tgo为预估的领弹飞行时间,h为设定的时间步长;
其中:n为取遍[1,2,…,N]的整数,当领弹飞过一个时间步长时,n取1,当领弹飞过两个时间步长时,n取2,并依次类推,直至领弹飞过N个时间步长,n取N为止。
采用上述方法改进后的虚拟点轨迹先弯曲再平直,从而降低了对从弹需用过载及控制能量的要求。
步骤III、在地面坐标系中建立从弹的运动模型为:
其中:Xm=[xm,ym,zm]表示从弹的位置,V为从弹的速度,θ和ψV为从弹的弹道倾角和弹道偏角。
步骤IV、根据步骤I-III所建立的模型,在地面坐标系中建立从弹与虚拟点之间的相对运动模型;
从弹和虚拟点之间的相对位置为:
对上式求导可得到从弹与虚拟点的相对速度差:
将其写为向量形式为:
其中Xd=[xd yd zd]T,T4=[-cosεycosεz -sinεy cosεysinεz]T, 领弹与目标之间的距离的变化率。
步骤102、建立描述从弹运动的质心动力学方程、姿态运动学方程以及姿态动力学方程,结合以上推导的从弹与虚拟点的相对运动模型,得到对从弹攻击角度和攻击时间进行控制的非线性控制模型,基于反馈线性化理论对所述非线性控制模型进行精确线性化,获取线性控制模型。
以下对本步骤的具体过程进行说明。
(I)将描述虚拟点和从弹相对运动的方程和从弹的质心动力学方程结合起来,进行精确线性化。
从弹的质心动力学方程为:
其中:m为从弹的质量,a为从弹的攻角,β为从弹的侧滑角,γV为从弹的倾斜角,g为重力加速度,P为从弹发动机的推力,X、Y、Z分别是从弹的阻力、升力和侧向力,其表达式为:
其中:cx、cy、cz分别是从弹的阻力系数、升力系数和侧向力系数,其可以根据风洞试验获取; 是从弹的动压,ρ是大气密度,S是从弹的特征面积。
将推力P作为控制量,然后将式(9)变形为:
为了表述方便,令
则,式(11)结合第(6)式,得到
接下来基于反馈线性化理论对式(12)进行精确线性化。设输出为控制模型中从弹与虚拟点的相对距离,即y=Xd=[xd yd zd]T,对控制模型中质心动力学方程进行微分同胚坐标变换,有:
一种控制多枚导弹攻击角度和攻击时间的方法专利购买费用说明
Q:办理专利转让的流程及所需资料
A:专利权人变更需要办理著录项目变更手续,有代理机构的,变更手续应当由代理机构办理。
1:专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。
2:按规定缴纳著录项目变更手续费。
3:同时提交相关证明文件原件。
4:专利权转移的,变更后的专利权人委托新专利代理机构的,应当提交变更后的全体专利申请人签字或者盖章的委托书。
Q:专利著录项目变更费用如何缴交
A:(1)直接到国家知识产权局受理大厅收费窗口缴纳,(2)通过代办处缴纳,(3)通过邮局或者银行汇款,更多缴纳方式
Q:专利转让变更,多久能出结果
A:著录项目变更请求书递交后,一般1-2个月左右就会收到通知,国家知识产权局会下达《转让手续合格通知书》。
![]()
动态评分
0.0