专利摘要

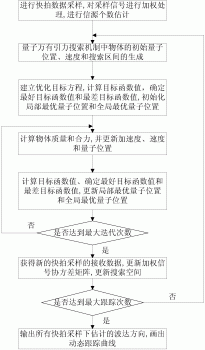
本发明涉及一种通过量子万有引力搜索机制和加权信号协方差极大似然方程的动态更新共同来实现的考虑在冲击噪声环境下对动态目标的波达方向进行鲁棒跟踪的冲击噪声环境下的量子万有引力搜索动态DOA估计方法。本发明包括：对空间D个信源信号进行快拍采样和加权处理；量子万有引力搜索机制的所有物体初始状态确定；确定最好目标函数值和最差目标函数值；计算在t次迭代的每个物体质量；计算目标函数值；判断是否达到最大迭代次数；对采样数据进行加权处理；判断最大跟踪次数；输出动态跟踪结果。本发明解决了冲击噪声环境下的动态目标方向跟踪问题，使用所设计的量子万有引力搜索机制作为搜索策略，所设计的方法具有快速和鲁棒性高的优点。

权利要求

1.一种冲击噪声环境下的量子万有引力搜索动态DOA估计方法，其特征在于： 

步骤一，对空间D个信源信号进行快拍采样和加权处理，由M个全向阵元构成的无模糊线阵，D个中心频率相同的远场窄带信号从方向{θ₁,θ₂,…,θ_D}入射到阵列上，阵列接收第k次快拍采样数据为x(k)＝As(k)+n(k)，式中x(k)＝[x₁(k),x₂(k),…,x_M(k)]^T为阵列的接收数据矢量；A(θ)＝[a(θ₁) a(θ₂) … a(θ_D)]是信号导向矢量矩阵，θ＝(θ₁,θ₂,…,θ_D)是角度矢量，θ_d（d＝1,2,…,D）是第d个信源的来波方向；s(t)＝[s₁(t),s₂(t),…,s_D(t)]^T为信号矢量； 

n(k)＝[n₁(k),n₂(k),…,n_M(k)]^T是独立同分布的满足SαS分布的冲击噪声向量；第d个导向矢量为a(θ_d)＝[exp(-jω₀τ_1d),exp(-jω₀τ_2d),…,exp(-jω₀τ_Md)]^Τ，d＝1,2,…,D，式中，  c为光速，f为入射信号的频率，λ为入射信号的波长， (l＝1,2,…,M)表示第d个信号到达第l个阵元时相对于参考阵元的时延，E_l为第l个阵元的位置，接收数据的加权信号为h(k)＝x(k)/max{|x₁(k)|^0.7,|x₂(k)|^0.7,…,|x_M(k)|^0.7}，max{}为取最大值函数，定义阵元接收数据之间的加权信号协方差为C(k)，第一次采样数据的加权信号协方差为C(1)＝h(1)h^H(1)，根据经典信息论准则估计信源个数D，t代表量子万有引力搜索机制的迭代次数，初始时设t＝0； 

步骤二，量子万有引力搜索机制的所有物体初始状态确定，由N个物体组成的系统，每个物体在D维搜索空间中运动，第i个物体的量子位置定义如下： 

(i＝1,2,…,N)， 为有效量子位置， 为辅助量子位置，0≤y_id(t)≤1(d＝1,2,…,D)表示第i个物体在第d维的有效量子位，z_id为第i个物体在第d维的辅助量子位，[y_id(t)]²+[z_id(t)]²＝1，把第i个物体的量子位置第一行即有效量子位置影射到定义区间，就是物体的当前位置q_i(t)＝[q_i1(t),q_i2(t),…,q_iD(t)]，对于所有的i＝1,2,…,N，q_id(t)＝y_id(t)[u_d(k)-l_d(k)]+l_d(k)，d＝1,2,…,D，第i个物体对应的速度为v_i(t)＝[v_i1(t),v_i2(t),…,v_iD(t)]，-0.2≤v_id(t)≤0.2(d＝1,2,…,D)表示第i个物体的第d维速度，t代表迭代次数，量子位置在定义的量子域[0，1]间随机初始化，在[-0.2，0.2]随机初始 化速度的每一维，确定初始搜索空间 为D个角度的搜索区间向量，u_d(k)和l_d(k)分别为第k次采样数据处理第d维的角度搜索区间的上限和下限值，最大迭代次数设置为 ，其中 为取整函数，zz为取整倍数； 

步骤三，第i个物体位置q_i(t)＝[q_i1(t),q_i2(t),…,q_iD(t)]的加权信号协方差极大似然方程的目标函数值为 ，正交投影矩阵  ，tr()表示矩阵的求迹运算，根据目标函数  评价物体位置的优劣， 代表有效量子位置  映射到搜索范围中的位置计算的目标函数值，即把 影射到参数范围后，使用fit[q_i(t)]计算物体的目标函数值，第i个物体到现在为止所经历的最优量子位置的第一行定义为该物体的局部最优位置，记作p_i(t)＝[p_i1(t),p_i2(t),…,p_iD(t)]，p_id(t)为第i个物体到第t次迭代为止所经历最优有效第d维量子位，d＝1,2,…,D，所有物体到现在所经历最优量子位置的第一行记作全局最优量子位置，也就是目标函数值最大的有效量子位置，记作b(t)＝[b₁(t),b₂(t),…,b_D(t)]，b_d(t)为所有物体到第t次迭代为止所经历最优有效第d维量子位，d＝1,2,…,D，确定最好目标函数值best(t)和最差目标函数值worst(t)， 

步骤四，计算在t次迭代的每个物体质量：M_ai＝M_pi＝M_ii＝M_i,i＝1,2,…,N,  M_pi表示被作用物体i的质量，M_ai表示作用到物体i的质量，M_ii为物体i的引力质量，M_i(t)为第i个物体的惯性质量，计算N个物体的万有引力的合力，对于第d维，第j个物体作用在第i个物体上的引力大小为  引力系数 T为最大迭代次数，R_ij(t)是第j个物体和第i个物体的欧氏距离，G₀和γ为常系数，R_ij(t)＝||p_i(t),p_j(t)||₂，对于 第d维，作用在第i个物体上的总作用力 i＝1,2,…,N，d＝1,2,…,D，rand_j是[0，1]间的随机数，更新所有物体的加速度、速度和量子位置，第i个物体的第d维加速度为 前N/2个物体速度根据引力方程进行更新，则第i个物体的第d维速度更新为  i＝1,2,…,N/2，d＝1,2,…,D；其他N/2个物体速度根据群行为进行更新，则第i个物体的第d维速度更新为v_id(t+1)＝c₄r₄[b_d(t)-y_id(t)]+c₅r₅[p_id(t)-y_id(t)]+w_tv_id(t)，w_t从初次迭代的0.9线形递减到最大迭代的0.5，i＝N/2+1,N/2+2,…,N，d＝1,2,…,D，r₁、r₂、r₃、r₄和r₅都是[0，1]之间的均匀随机数，加权常数c₁＝c₂＝c₄＝c₅＝0.78，c₃＝0.1；对于v_id(t+1)，若超出边界值，将其限制在边界，即v_id(t+1)＞0.2，v_id(t+1)＝0.2，若v_id(t+1)<-0.2，v_id(t+1)＝-0.2，量子位置为 i＝1,2,…,N，其中  d＝1,2,…,D，abs()为量子位取绝对值函数； 

步骤五，量子位置y_i(t+1)影射到定义区间q_i(t+1)，计算目标函数值， 

i＝1,2,…,N，d＝1,2,…,D，若 

fit[q_i(t+1)]＞fitq[p_i(t)]，则令局部最优量子位置 否则, 

p_i(t+1)＝p_i(t)，把最优的局部最优量；子位置设置成全局最优量子位置为 

b(t+1)＝[b₁(t+1),b₂(t+1),…,b_D(t+1)]，确定当前最好目标函数值best(t+1)和最差目标函数值worst(t+1)，

步骤六，判断是否达到最大迭代次数，若是，记录最优位置，执行步骤七；否则，t＝t+1，返回步骤四； 

步骤七，快拍采样新数据x(k+1)＝[x₁(k+1),x₂(k+1),…,x_M(k+1)]^T，对采样数据进行加权处 理：h(k+1)＝x(k+1)/max{|x₁(k+1)|^0.7,|x₂(k+1)|^0.7,…,|x_M(k+1)|^0.7}，计算当前采样的加权信号协方差： 其中 是新增加的第k+1个采样数据的加权信号协方差的增量，更新搜索空间为Z(k+1)，  d＝1,2,…,D，β为收敛因子，决定了搜索空间的收敛速度；常数r为搜索空间在锁定状态下的搜索半径； 为第d个方向在第k次采样时的估计值； 为第d个方向在第k次采样时搜索空间的中心值，其更新公式为 其中δ为遗传因子； 

步骤八，如果达到最大跟踪次数，执行步骤九；否则，设k＝k+1，t＝0，返回步骤二继续估计动态目标下一个时刻的方向； 

步骤九，得到所有快拍采样下的全局最优位置就是检测的动态目标方向值，输出动态跟踪结果。 

说明书

技术领域

本发明涉及一种通过量子万有引力搜索机制和加权信号协方差极大似然方程的动态更新共同来实现的考虑在冲击噪声环境下对动态目标的波达方向进行鲁棒跟踪的冲击噪声环境下的量子万有引力搜索动态DOA估计方法。

背景技术

动态DOA估计技术作为无线通信系统、雷达和导弹制导的关键技术，是决定能否快速跟踪信源信号，实现精确定位的关键。子空间更新算法是动态DOA估计领域中研究的重点。其中子空间更新算法按其原理可分成三类：第一类是静态的DOA估计方法直接推广，如幂迭代算法等基于特征分解批处理的子空间更新算法。第二大类是是将空间谱估计中的求解子空间更新问题转化为最优化问题，然后求出最优解。如带约束的最优化问题梯度法和无约束的最优化问题的投影逼近子空间跟踪。第三类是基于秩-1子空间更新算法，分别将协方差矩阵的信号子空间及噪声子空间进行平均，从而得到一个秩等于2的矩阵，数据的更新就是对这个矩阵的更新，典型算法如ROSA算法等。基于子空间的动态DOA估计虽具有计算量小，处理速度快的特点，但步骤繁琐，在相干信源跟踪场合还需引入空间平滑等解相干算法，可能会带来有效孔径的损失；而且在低信噪比情况下的跟踪性能并不理想。最大似然算法作为一种经典的DOA估计方法，不仅具有优越的估计性能和解相干的能力。而且该算法直接能处理数据协方差矩阵，在动态DOA估计中能避免子空间类跟踪方法需要不断重复的协方差矩阵分解问题，可节省计算量。

经对现有技术文献的检索发现，刁鸣等在《系统工程与电子技术》(2009,Vol.29,No.12,pp.2046–2049)上发表的“一种新的基于粒子群算法的DOA跟踪方法”中使用了粒子群算法和极大似然算法进行相干信号的动态DOA估计，在高斯噪声背景下效果较好，但在冲击噪声背景下，方法性能恶化严重导致失效。赵大勇等在《山东大学学报》(2010,Vol.40,No.1,pp.133-138)上发表的“冲击噪声背景下的动态DOA跟踪”提出了粒子群算法和分数低阶矩的极大似然方法求解弱冲击噪声环境下的动态DOA估计问题，使用分数低阶矩的动态更新能在一定程度上实现动态DOA估计问题，但计算时间较长，依旧不能解决冲击噪声环境下的动态DOA估计的收敛速度和精度问题，在特征指数小于1的强冲击噪声情况下基于粒子群算法和分数低阶矩的极大似然方法就失效了。

已有文献表明，在恶劣噪声环境下，动态DOA估计问题依旧没有解决。针对冲击噪声环境下的DOA估计是一个难题，尤其对相干信源的动态跟踪更难，故不能把高斯噪声环境下的DOA估计算法直接进行移植。在冲击噪声下的鲁棒动态DOA估计首先应能建立高性能的鲁棒动态跟踪的优化方程，冲击噪声环境下经典智能计算方法很难摆脱收敛速度和收敛性能矛盾的制约，在现有计算条件下很难在有限的时间内搜索到最优解，需要设计新的智能算法求解冲击噪声环境特别是强冲击噪声环境下的鲁棒动态DOA估计问题。

运用空间平滑等解相干技术对数据协方差矩阵进行预处理虽能解相干但损失阵列孔径。而极大似然估计算法作为一种经典的DOA估计方法，在高斯噪声环境下不仅具有优越的估计性能，还避免了子空间跟踪类方法需要不断重复协方差矩阵分解的问题。但极大似然算法角度估计的另一缺点是搜索过程是一个复杂耗时的过程，运算量巨大。因此，本专利在冲击噪声环境提出了一种基于加权信号协方差的极大似然算法的动态DOA估计方法。该方法先将目标锁定在一个变化的搜索范围之内，再设计量子万有引力搜索机制在该搜索空间搜索加权信号极大似然方程的所蕴含的最优角度。通过逐渐减小搜索的范围以及运用智能搜索机制，有效解决了搜索方法的计算量问题。仿真结果表明这种冲击噪声环境下的动态目标DOA估计方法能够保证所设计方法的实时性，而且具备解相干的能力和较好的跟踪精度，尤其在小特征指数情况下，有非常明显的优势。

发明内容

本发明的目的在于提供一种有效性和鲁棒性更高的冲击噪声环境下的量子万有引力搜索动态DOA估计方法。

本发明的目的这样实现的：

步骤一，对空间D个信源信号进行快拍采样和加权处理，由M个全向阵元构成的无模糊线阵，D个中心频率相同的远场窄带信号从方向{θ₁,θ₂,…,θ_D}入射到阵列上，阵列接收第k次快拍采样数据为x(k)=As(k)+n(k)，式中x(k)=[x₁(k),x₂(k),…,x_M(k)]^T为阵列的接收数据矢量；A(θ)=[a(θ₁) a(θ₂) … a(θ_D)]是信号导向矢量矩阵，θ=(θ₁,θ₂,…,θ_D)是角度矢量，θ_d（d=1,2,…,D）是第d个信源的来波方向；s(t)=[s₁(t),s₂(t),…,s_D(t)]^T为信号矢量；

n(k)=[n₁(k),n₂(k),…,n_M(k)]^T是独立同分布的满足SαS分布的冲击噪声向量；第d个导向矢量为a(θ_d)=[exp(-jω₀τ_1d),exp(-jω₀τ_2d),…,exp(-jω₀τ_Md)]^Τ，d=1,2,…,D，式中， c为光速，f为入射信号的频率，λ为入射信号的波长， (l=1,2,…,M)表示第d个信号到达第l个阵元时相对于参考阵元的时延，E_l为第l个阵元的位置，接收数据的加权信号为h(k)=x(k)/max{|x₁(k)|^0.7,|x₂(k)|^0.7,…,|x_M(k)|^0.7}，max{}为取最大值函数，定义阵元接收数据之间的加权信号协方差为C(k)，第一次采样数据的加权信号协方差为C(1)=h(1)h^H(1)，根据经典信息论准则估计信源个数D，t代表量子万有引力搜索机制的迭代次数，初始时设t=0；

步骤二，量子万有引力搜索机制的所有物体初始状态确定，由N个物体组成的系统，每个物体在D维搜索空间中运动，第i个物体的量子位置定义如下：

yi(t)=y‾i(t)z‾i(t)=yi1(t),yi2(t),...,yiD(t)zi1(t),zi2(t),...,ziD(t),]]>(i=1,2,…,N)， 为有效量子位置， 为辅助量子位置，0≤y_id(t)≤1(d=1,2,…,D)表示第i个物体在第d维的有效量子位，z_id为第i个物体在第d维的辅助量子位，[y_id(t)]²+[z_id(t)]²=1，把第i个物体的量子位置第一行即有效量子位置影射到定义区间，就是物体的当前位置q_i(t)=[q_i1(t),q_i2(t),…,q_iD(t)]，对于所有的i=1,2,…,N，q_id(t)=y_id(t)[u_d(k)-l_d(k)]+l_d(k)，d=1,2,…,D，第i个物体对应的速度为v_i(t)=[v_i1(t),v_i2(t),…,v_iD(t)]，-0.2≤v_id(t)≤0.2(d=1,2,…,D)表示第i个物体的第d维速度，t代表迭代次数，量子位置在定义的量子域[0，1]间随机初始化，在[-0.2，0.2]随机初始化速度的每一维，确定初始搜索空间Z(k)=u1(k)u2(k)...uD(k)l1(k)l2(k)...lD(k)]]>为D个角度的搜索区间向量，u_d(k)和l_d(k)分别为第k次采样数据处理第d维的角度搜索区间的上限和下限值，最大迭代次数设置为 ，其中 为取整函数，zz为取整倍数；

步骤三，第i个物体位置q_i(t)=[q_i1(t),q_i2(t),…,q_iD(t)]的加权信号协方差极大似然方程的目标函数值为fit(qi(t))=tr[PA[qi(t)]C(k)]]]>，正交投影矩阵PA[qi(t)]=A(qi(t))[AH(qi(t))A(qi(t))]-1AH(qi(t))]]>，tr()表示矩阵的求迹运算，根据目标函数fitq[y‾i(t)]=fit[qi(t)]=tr[PA[qi(t)]C(k)]]]>评价物体位置的优劣， 代表有效量子位置 映射到搜索范围中的位置计算的目标函数值，即把 影射到参数范围后，使用fit[q_i(t)]计算物体的目标函数值，第i个物体到现在为止所经历的最优量子位置的第一行定义为该物体的局部最优位置，记作p_i(t)=[p_i1(t),p_i2(t),…,p_iD(t)]，p_id(t)为第i个物体到第t次迭代为止所经历最优有效第d维量子位，d=1,2,…,D，所有物体到现在所经历最优量子位置的第一行记作全局最优量子位置，也就是目标函数值最大的有效量子位置，记作b(t)=[b₁(t),b₂(t),…,b_D(t)]，b_d(t)为所有物体到第t次迭代为止所经历最优有效第d维量子位，d=1,2,…,D，确定最好目标函数值best(t)和最差目标函数值worst(t)，

best(t)=maxj∈{1,2,...,N}{fitq(pj(t))},]]>worst(t)=minj∈{1,2,...,N}{fitq(pj(t))};]]>

步骤四，计算在t次迭代的每个物体质量：M_ai=M_pi=M_ii=M_i,i=1,2,…,N,mi(t)=fitq[pi(t)]-worst(t)best(t)-worst(t),]]>Mi(t)=mi(t)Σj=1Nmj(t),]]>M_pi表示被作用物体i的质量，M_ai表示作用到物体i的质量，M_ii为物体i的引力质量，M_i(t)为第i个物体的惯性质量，计算N个物体的万有引力的合力，对于第d维，第j个物体作用在第i个物体上的引力大小为Fijd(t)=G(t)Mpi(t)×Maj(t)Rij(t)+ϵ[pjd(t)-pid(t)],]]>引力系数G(t)=G0e-γtT,]]>T为最大迭代次数，R_ij(t)是第j个物体和第i个物体的欧氏距离，G₀和γ为常系数，R_ij(t)=||p_i(t),p_j(t)||₂，对于第d维，作用在第i个物体上的总作用力 i=1,2,…,N，d=1,2,…,D，rand_j是[0，1]间的随机数，更新所有物体的加速度、速度和量子位置，第i个物体的第d维加速度为 前N/2个物体速度根据引力方程进行更新，则第i个物体的第d维速度更新为vid(t+1)=c1r1[bd(t)-yid(t)]+c2r2[pid(t)-yid(t)]+c3[r3vid(t)+aid(t)],]]>i=1,2,…,N/2，d=1,2,…,D；其他N/2个物体速度根据群行为进行更新，则第i个物体的第d维速度更新为v_id(t+1)=c₄r₄[b_d(t)-y_id(t)]+c₅r₅[p_id(t)-y_id(t)]+w_tv_id(t)，w_t从初次迭代的0.9线形递减到最大迭代的0.5，i=N/2+1,N/2+2,…,N，d=1,2,…,D，r₁、r₂、r₃、r₄和r₅都是[0，1]之间的均匀随机数，加权常数c₁=c₂=c₄=c₅=0.78，c₃=0.1；对于v_id(t+1)，若超出边界值，将其限制在边界，即v_id(t+1)>0.2，v_id(t+1)=0.2，若v_id(t+1)<-0.2，v_id(t+1)=-0.2，量子位置为yi(t+1)=yi1(t+1),yi2(t+1),...,yiD(t+1)zi1(t+1),zi2(t+1),...,ziD(t+1),]]>i=1,2,…,N，其中yid(t+1)zid(t+1)=abs(cos(-vid(t+1))-sin(-vid(t+1))sin(-vid(t+1))cos(-vid(t+1))yid(t)zid(t)),]]>d=1,2,…,D，abs()为量子位取绝对值函数；

步骤五，量子位置y_i(t+1)影射到定义区间q_i(t+1)，计算目标函数值，

fitq[y‾i(t+1)]=fit[qi(t+1)]=tr[PA[qi(t+1)]C(t)],]]>i=1,2,…,N，d=1,2,…,D，若

fit[q_i(t+1)]>fitq[p_i(t)]，则令局部最优量子位置 否则,

p_i(t+1)=p_i(t)，把最优的局部最优量；子位置设置成全局最优量子位置为

b(t+1)=[b₁(t+1),b₂(t+1),…,b_D(t+1)]，确定当前最好目标函数值best(t+1)和最差目标函数值worst(t+1)，best(t+1)=maxj∈{1,2,...,N}{fitq(pj(t+1))},]]>worst(t+1)=minj∈{1,2,...,N}{fitq(pj(t+1))};]]>

步骤六，判断是否达到最大迭代次数，若是，记录最优位置，执行步骤七；否则，t=t+1，返回步骤四；

步骤七，快拍采样新数据x(k+1)=[x₁(k+1),x₂(k+1),…,x_M(k+1)]^T，对采样数据进行加权处理：h(k+1)=x(k+1)/max{|x₁(k+1)|^0.7,|x₂(k+1)|^0.7,…,|x_M(k+1)|^0.7}，计算当前采样的加权信号协方差：C(k+1)=μC(k)+(1-μ)C^(k+1),]]>其中C^(k+1)=h(k+1)hH(k+1)]]>是新增加的第k+1个采样数据的加权信号协方差的增量，更新搜索空间为Z(k+1)，ld(k+1)=θ‾d,e(k)-βk|ld(k)-θ‾d(k)|-r,]]>ud(k+1)=θ‾d,e(k)+βk|ud(k)-θ‾d(k)|+r,]]>d=1,2,…,D，β为收敛因子，决定了搜索空间的收敛速度；常数r为搜索空间在锁定状态下的搜索半径； 为第d个方向在第k次采样时的估计值； 为第d个方向在第k次采样时搜索空间的中心值，其更新公式为θ‾d,e(k+1)=δθ‾d,e(k)+(1-δ)θ‾d(k),]]>其中δ为遗传因子；

步骤八，如果达到最大跟踪次数，执行步骤九；否则，设k=k+1，t=0，返回步骤二继续估计动态目标下一个时刻的方向；

步骤九，得到所有快拍采样下的全局最优位置就是检测的动态目标方向值，输出动态跟踪结果。

本发明的有益效果在于：

(1)本发明解决了冲击噪声环境下的动态目标方向跟踪问题，使用所设计的量子万有引力搜索机制作为搜索策略，所设计的方法具有快速和鲁棒性高的优点。

(2)相对于现有的弱冲击噪声环境下的动态目标跟踪方法，本发明可以同时利用量子万有引力搜索机制和加权信号协方差极大似然优化方程的优势解决高斯噪声和冲击噪声环境下的动态目标跟踪问题，且适用于特征指数小于1的恶劣冲击噪声环境，说明本方法的适用性更广。

(3)实验结果表明，本发明所提出的量子万有引力DOA估计方法在对动态目标跟踪时能够得到最优解，但时间开销远小于已有极大似然测向方法，估计精度却优于现有的极大似然方法，说明了所提鲁棒动态跟踪方法的有效性。

附图说明

图1为量子万有引力动态DOA估计的跟踪方法示意图。

图2为量子万有引力搜索机制的结构示意图。

图3为特征指数α=1.4时两个独立信源的粒子群算法和分数低阶矩极大似然算法的动态DOA估计跟踪情况。

图4为特征指数α=1.4时对于两个独立信源所提的量子万有引力动态DOA估计方法的角度跟踪情况。

图5为特征指数α=1.4时两个相干信源粒子群算法和分数低阶矩极大似然算法的动态DOA估计跟踪情况。

图6为特征指数α=1.4时对于两相干源所提的量子万有引力动态DOA估计方法的角度跟踪情况。

图7为特征指数α=0.9时两个独立信源的基于粒子群算法和分数低阶矩极大似然算法的动态跟踪情况。

图8为特征指数α=0.9时两个独立信源的所提的量子万有引力动态DOA估计方法的角度跟踪情况。

图9为量子万有引力动态DOA估计方法的总体结构图。

具体实施方式

下面结合附图对本发明做进一步描述。

本发明针对现有冲击噪声环境下动态跟踪方法的不足，提出了一种可在复杂噪声环境和恶劣测向背景达到鲁棒跟踪的动态目标跟踪方法。该方法先设计一种加权信号协方差的更新方法，并提出解决连续优化问题的量子万有引力搜索算法去求解动态目标跟踪。在工程应用中，当冲击噪声的特征指数为2时满足高斯噪声分布函数形式，故本发明所提出的方法也能够解决高斯噪声环境的动态跟踪问题。

本发明是通过如下技术方案来实现的，主要包括以下步骤：

步骤一，对空间D个信源信号进行快拍采样和加权处理。由M个全向阵元构成的无模糊线阵，D个中心频率相同的远场窄带信号从方向{θ₁,θ₂,…,θ_D}入射到阵列上，阵列接收第k次快拍采样数据为x(k)=As(k)+n(k)，式中x(k)=[x₁(k),x₂(k),…,x_M(k)]^T为阵列的接收数据矢量；A(θ)=[a(θ₁) a(θ₂) … a(θ_D)]是信号导向矢量矩阵，θ=(θ₁,θ₂,…,θ_D)是角度矢量，θ_d（d=1,2,…,D）是第d个信源的来波方向；s(t)=[s₁(t),s₂(t),…,s_D(t)]^T为信号矢量；n(k)=[n₁(k),n₂(k),…,n_M(k)]^T是独立同分布的满足SαS分布的冲击噪声向量；第d个导向矢量为a(θ_d)=[exp(-jω₀τ_1d),exp(-jω₀τ_2d),…,exp(-jω₀τ_Md)]^Τ，d=1,2,…,D，式中， c为光速，f为入射信号的频率，λ为入射信号的波长， (l=1,2,…,M)表示第d个信号到达第l个阵元时相对于参考阵元的时延，E_l为第l个阵元的位置。接收数据的加权信号为h(k)=x(k)/max{|x₁(k)|^0.7,|x₂(k)|^0.7,…,|x_M(k)|^0.7}，max{}为取最大值函数。定义阵元接收数据之间的加权信号协方差为C(k)，第一次采样数据的加权信号协方差为C(1)=h(1)h^H(1)。根据经典信息论准则估计信源个数D。t代表量子万有引力搜索机制的迭代次数，初始时设t=0

步骤二，量子万有引力搜索机制的所有物体初始状态确定。考虑由N个物体组成的系统，每个物体在D维搜索空间中运动，物体的位置代表优化问题的解。第i个物体的量子位置定义如下:yi(t)=y‾i(t)z‾i(t)=yi1(t),yi2(t),...,yiD(t)zi1(t),zi2(t),...,ziD(t),]]>(i=1,2,…,N)，其中: 为有效量子位置， 为辅助量子位置，0≤y_id(t)≤1(d=1,2,…,D)表示第i个物体在第d维的有效量子位，z_id为第i个物体在第d维的辅助量子位，[y_id(t)]²+[z_id(t)]²=1，把第i个物体的量子位置第一行即有效量子位置影射到定义区间，就是该物体的当前位置

q_i(t)=[q_i1(t),q_i2(t),…,q_iD(t)]，对于所有的i=1,2,…,N，

q_id(t)=y_id(t)[u_d(k)-l_d(k)]+l_d(k)，d=1,2,…,D，第i个物体对应的速度为

v_i(t)=[v_i1(t),v_i2(t),…,v_iD(t)]，-0.2≤v_id(t)≤0.2(d=1,2,…,D)表示第i个物体的第d维速度，t代表迭代次数。为了使初始位置具有一定的分散性和均布性，量子位置在定义的量子域[0，1]间随机初始化，在[-0.2，0.2]随机初始化速度的每一维。确定初始搜索空间Z(k)=u1(k)u2(k)...uD(k)l1(k)l2(k)...lD(k)]]>为D个角度的搜索区间向量，u_d(k)和l_d(k)分别为第k次采样数据处理第d维的角度搜索区间的上限和下限值，最大迭代次数设置为 ，其中 为取整函数，zz为取整倍数。

步骤三，第i个物体位置q_i(t)=[q_i1(t),q_i2(t),…,q_iD(t)]的加权信号协方差极大似然方程的目标函数值为 ，式中，正交投影矩阵PA[qi(t)]=A(qi(t))[AH(qi(t))A(qi(t))]-1AH(qi(t))]]>，tr()表示矩阵的求迹运算，目标函数值越大，量子位置和位置越优秀，估计角度越准确。根据目标函数fitq[y‾i(t)]

一种冲击噪声环境下的量子万有引力搜索动态DOA估计方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。