专利摘要

本发明涉及一种L阵方位角和俯仰角配对的信号处理方法，属于无线电信号处理领域；用于当L阵二维波达角估计问题分解为两个一维波达角估计时产生的配对问题；本发明的目的是在测出两组一维波达角基础上实现它们之间的自动配对；两组一维波达角的估计与配对算法独立进行，基于最大似然准则配对使得本发明具有较高的鲁棒性；本发明的优势在于：本发明的配对与一维波达角估计独立进行，配对方法处理过程不受一维波达角估计过程的影响，本发明在低信噪比和小快拍数条件下依然具有较高鲁棒性，在相干源和非均匀L阵条件下，该配对方法依然适用。

权利要求

1.一种L阵方位角和俯仰角配对的信号处理方法，其特征在于：

本信号处理方法的基本步骤为：

步骤一：预处理，根据已有的一维线阵波达角估计方法得出目标与两个线阵的两组一维波达角；设两线阵X、Y相交于原点，阵元数分别为M+1、N+1，总阵元数为M+N+1；设有K个同中心频率的远场窄带信号被该L阵接收，λ为载频波长，θ_k和 分别表示第k个来波信号的方位角和俯仰角(θ∈[0,2π], )，设信源在两个线阵上是可分的，此时将L阵的二维波达角估计问题被分解为两个一维波达角估计；

记a_x,a_y为线阵X、Y的导向矢量，x_m为X轴上第m个阵元到原点的距离(m=1,2,…M)，y_n为Y轴上第n个阵元到原点的距离(n=1,2,…,N)，则信源k的导向矢量可以表示为：

$\left\{\begin{array}{cc}{a}_x\left({\alpha }_k\right)={[1{,e}^{-j\frac{2\pi x_1}{\lambda }\cos {\alpha }_k},e^{-j\frac{2\pi x_2}{\lambda }\cos {\alpha }_k},···,e^{-j\frac{2\pi x_M}{\lambda }\cos {\alpha }_k}]}^T& k=\mathrm{1,2},···,K\\ a_y\left({\beta }_k\right)={[1{,e}^{-j\frac{2\pi y_1}{\lambda }\cos {\beta }_k},e^{-j\frac{2\pi y_2}{\lambda }\cos {\beta }_k},···,e^{-j\frac{2\pi y_N}{\lambda }\cos {\beta }_k}]}^T& k=\mathrm{1,2},···,K\end{array}\right.---\left(1\right)$

其中， 记A_x、A_y分别为线阵X和线阵Y的阵列流型，A_x(α)=[a_x(α₁),a_x(α₂),…,a_x(α_K)]，A_y(β)=[a_y(β₁),a_y(β₂),…,a_y(β_K)]；s_k为第k个信源的复包络，则回波信号可以表示为s(t)=[s₁(t),s₂(t),…,s_K(t)]^T；

记n_x,n_y为高斯白噪声，则X阵列和Y阵列的接收数据分别为：

$\left\{\begin{array}{c}X\left(t\right)=A_x\left(\alpha \right)s+n_x=\underset{k=1}{\overset{K}{\Sigma }}{a}_x\left({\alpha }_k\right)s_k\left(t\right)+n_x\left(t\right)\\ Y\left(t\right)=A_y\left(\beta \right)s+n_y=\underset{k=1}{\overset{K}{\Sigma }}{a}_y\left({\beta }_k\right)s_k\left(t\right)+n_y\left(t\right)\end{array}\right.---\left(2\right)$

采用一维波达角估计方法分别估计出目标与两个线阵X、Y的夹角 和

步骤二：用其中一个线阵的接收数据和该线阵所估计的一维波达角得到一个信源协方差矩阵；在高斯白噪声背景下，第一个信源协方差矩阵 的最大似然估计表示为：

${\hat{R}}_s=E\left\{\hat{s}{\hat{s}}^H\right\}=E\{{\hat{A}}_y^{+}·{\mathrm{YY}}^H·{\left({\hat{A}}_y^H\right)}^{+}\}={\hat{A}}_y^{+}{R}_{\mathrm{yy}}{\left({\hat{A}}_y^H\right)}^{+}---\left(4\right)$

其中 为由线阵Y所估计的 构造的阵列流型， 中各角度的顺序任意， 为 的Moore-Penrose逆，R_yy为线阵Y接收数据的协方差矩阵：

$R_{\mathrm{yy}}=E\left\{{\mathrm{YY}}^H\right\}=A_y·E\left\{{\mathrm{ss}}^H\right\}·A_y^H+{\sigma }^{2}I=A_y{R}_s{A}_y^H+{\sigma }^{2}I---\left(5\right)$

步骤三：同时用两个线阵的接收数据和所估计的两组一维波达角获得第二个信源协方差矩阵；对线阵X，记与 相对应的线阵X的阵列流型为 若 为 的后N行，第二个信源协方差矩阵为：

$\begin{array}{c}{R}_s^{\prime }={\hat{A}}_x^{+}·E\left\{{\mathrm{XY}}^H\right\}·{\left({\hat{A}}_y^{\prime H}\right)}^{+}\\ ={\hat{A}}_x^{+}+R_{\mathrm{xy}}{\left({\hat{A}}_y^{\prime H}\right)}^{+}\end{array}---\left(6\right)$

其中 Y′分别为A_y、Y的后N行；

步骤四：利用一个置换矩阵将两个信源协方差矩阵等价连接起来，通过优化方法得出一一对应的两组一维波达角；定义一K×K维置换矩阵T，若T_ij为矩阵T的第i行j列元素，则

$\left\{\begin{array}{cc}\forall T_{\mathrm{ij}}\in \left\{\mathrm{0,1}\right\}& \\ \underset{i=1}{\overset{K}{\Sigma }}{T}_{\mathrm{ij}}=1& j=\mathrm{1,2},···,K\\ \underset{j=1}{\overset{K}{\Sigma }}{T}_{\mathrm{ij}}=1& i=\mathrm{1,2},···,K\end{array}\right.---\left(7\right)$

若保持 的顺序不变，相对应的来波与阵列X的夹角为[α₁,α₂,…,α_K]^T，则两线阵对应的阵列流型为 若 则 式(6)可化为

$R_s^{\prime }={\hat{A}}_x^{+}{R}_{\mathrm{xy}}{\left({\hat{A}}_y^{\prime H}\right)}^{+}\approx {\mathrm{TA}}_x^{+}\left(A_x{R}_s{A}_y^{\prime H}\right){\left({\hat{A}}_y^{\prime H}\right)}^{+}\approx {\mathrm{TR}}_s\approx T{\hat{R}}_s---\left(8\right)$

当信源独立时， 可以直接由 得出T，然后将T修正成式(7)所示的形式，即可得出 的对应关系；记

$J_{\mathrm{PMLS}}=\underset{T}{\min }{\left|\right|R_s^{\prime }-T{\hat{R}}_s\left|\right|}_F^2=\underset{T}{\min }{\left|\right|\left({\hat{A}}_x^{+}{R}_{\mathrm{xy}}{\left({\hat{A}}_y^{\prime H}\right)}^{+}\right)-T·\left({\hat{A}}_y^{+}{R}_{\mathrm{yy}}{\left({\hat{A}}_y^H\right)}^{+}\right)\left|\right|}_F^2---\left(9\right)$

上式只需求一次 的Moore-Penrose逆，因最多可存在K!种可能的配对情况，因此需进行K!次运算；当信源数K较大时，式(9)的运算量增加，进一步降维优化，若记T的第i行记为T_i， 的第i行记为 则

$J_{\mathrm{MPMLS}}=\underset{T_i}{\min }{\left|\right|R_{\mathrm{si}}^{\prime }-T_i{\hat{R}}_s\left|\right|}_F^2---\left(10\right)$

T_i的解为e₁=[10…0]，e₂=[01…0]，……，e_K=[00…1]中的一个，且T每行的解不一样，因此只需计算(K-1)(K+2)/2次式(10)即可得出T；

步骤五：根据两组一维波达角的空间几何关系得出目标的方位角和俯仰角；目标的方位角θ_k和俯仰角

得出θ_k后根据cosα_k,cosβ_k的正负确定θ_k在四个象限的位置，调整θ_k大小。

说明书

技术领域

本发明涉及一种L阵方位角和俯仰角配对的信号处理方法，属于无线电信号处理领域。

背景技术

L阵是由两个垂直相交的线阵构成的简单二维阵，可以同时得到目标的方位角和俯仰角，在二维波达角估计方面具有许多优点，近年来受到学者的广泛关注。工程中通常将L阵的二维波达角估计问题分解为两个线阵的一维波达角估计，然后对所估计的两组一维波达角通过配对得到无模糊的目标方位角和俯仰角，这样可以有效降低运算量等。

L阵配对方法目前大致可以分为三类：一、对由声学矢量传感器构成的阵列，可以直接利用传感器的空间矢量特性实现自动配对，不过该方法受传感器类型限制而适用范围有限。二、将两个一维波达角估计和配对过程融合在一起，这类方法通常要构造一个特殊的广义协方差矩阵，该协方差矩阵中含有两个线阵阵列流型之间的对应关系，利用这个对应关系实现配对，不过一般情况下这类方法由于协方差矩阵维数较大导致特征分解运算量变大，并且往往仅适用于均匀L阵和非相干源情况。三、先进行两组一维波达角估计，然后独立进行配对，如通过Toeplitz法估计出来波与两个线阵一维波达角的余弦差值，以该差值为媒介实现配对，该方法在相干源情况下同样有效，但两个线阵必须是均匀线阵，且由于Toeplitz法精度较差导致算法鲁棒性不高；先由所估计的两组一维波达角得出一个“信源协方差矩阵”，然后以该矩阵是否为Hermite矩阵为准则判断是否配对正确，不过等强度独立信源情况下算法鲁棒性稍差。

综上，目前L阵的二维波达角配对方法存在鲁棒性低、适用范围受限等缺点。基于此，本发明基于最大似然准则提出一种新的配对方法，该方法属于上述第三类，可实现在没有任何先验信息情况下目标配对，先进行两组一维波达角估计，然后利用这两组估计的一维波达角和两个线阵的接收数据得到两个信源协方差矩阵的最大似然估计，最后根据这两个协方差矩阵的置换关系通过优化的方法实现配对。相比已有配对方法，本发明所提的配对方法更加灵活，且在低信噪比和小快拍数情况仍有较高鲁棒性，对信源是否相干和阵列是否均匀没有特殊要求。

发明内容

本发明的目的是在测出两组一维波达角基础上实现它们之间的自动配对。两组一维波达角的估计与配对算法独立进行，使得本发明的适用范围更广，基于最大似然准则配对使得本发明具有较高的鲁棒性。假设两个线阵的目标数和一维波达角是先验知识或者已经估计出来的，且目标与两个线阵的夹角是可分辨的。

本发明的基本步骤为：

步骤一：预处理，根据已有的一维线阵波达角估计方法得出目标与两个线阵的两组一维波达角；设两线阵X、Y相交于原点，阵元数分别为M+1、N+1，总阵元数为M+N+1；设有K个同中心频率的远场窄带信号被该L阵接收，λ为载频波长，θ_k和 分别表示第k个来波信号的方位角和俯仰角(θ∈[0,2π], )，假设信源在两个线阵上是可分的，此时将L阵的二维波达角估计问题被分解为两个一维波达角估计；

记a_x,a_y为线阵X、Y的导向矢量，x_m为X轴上第m个阵元到原点的距离(m=1,2,LM)，y_n为Y轴上第n个阵元到原点的距离(n=1,2,L,N)，则信源k的导向矢量可以表示为：

ax(αk)=[1,e-j2πx1λcosαk,e-j2πx2λcosαk,···,e-j2πxMλcosαk]Tk=1,2,···,Kay(βk)=[1,e-j2πy1λcosβk,e-j2πy2λcosβk,···,e-j2πyNλcosβk]Tk=1,2,···,K---(1)]]>

其中， 记A_x、A_y分别为线阵X和线阵Y的阵列流型，A_x(α)=[a_x(α₁),a_x(α₂),…,a_x(α_K)]，A_y(β)=[a_y(β₁),a_y(β₂),…,a_y(β_K)]；s_k为第k个信源的复包络，则回波信号可以表示为s(t)=[s₁(t),s₂(t),…,s_K(t)]^T；

记n_x,n_y为高斯白噪声，则X阵列和Y阵列的接收数据分别为：

X(t)=Ax(α)s+nx=Σk=1Kax(αk)sk(t)+nx(t)Y(t)=Ay(β)s+ny=Σk=1Kay(βk)sk(t)+ny(t)---(2)]]>

采用一维波达角估计方法分别估计出目标与两个线阵X、Y的夹角 和

步骤二：用其中一个线阵的接收数据和该线阵所估计的一维波达角得到一个信源协方差矩阵；在高斯白噪声背景下，第一个信源协方差矩阵 的最大似然估计表示为：

R^s=E{s^s^H}=E{A^y+·YYH·(A^yH)+}=A^y+Ryy(A^yH)+---(4)]]>

其中 为由线阵Y所估计的 构造的阵列流型， 中各角度的顺序任意， 为 的Moore-Penrose逆，R_yy为线阵Y接收数据的协方差矩阵：

Ryy=E{YYH}=Ay·E{ssH}·AyH+σ2I=AyRsAyH+σ2I---(5)]]>

步骤三：同时用两个线阵的接收数据和所估计的两组一维波达角获得第二个信源协方差矩阵；对线阵X，记与 相对应的线阵X的阵列流型为 若 为 的后N行，第二个信源协方差矩阵为：

Rs′=A^x+·E{XYH}·(A^y′H)+=A^x++Rxy(A^y′H)+---(6)]]>

其中 Y′分别为A_y、Y的后N行；

步骤四：利用一个置换矩阵将两个信源协方差矩阵等价连接起来，通过优化方法得出一一对应的两组一维波达角；定义一K×K维置换矩阵T，若T_ij为矩阵T的第i行j列元素，则

∀Tij∈{0,1}Σi=1KTij=1j=1,2,···,KΣj=1KTij=1i=1,2,···,K---(7)]]>

若保持 的顺序不变，相对应的来波与阵列X的夹角为[α₁,α₂,…,α_K]^T，则两线阵对应的阵列流型为 若 则 式(6)可化为

Rs′=A^x+Rxy(A^y′H)+≈TAx+(AxRsAy′H)(A^y′H)+≈TRs≈TR^s---(8)]]>

当信源独立时， 可以直接由 得出T，然后将T修正成式(7)所示的形式，即可得出 的对应关系；记

JPMLS=minT||Rs′-TR^s||F2=minT||(A^x+Rxy(A^y′H)+)-T·(A^y+Ryy(A^yH)+)||F2---(9)]]>

上式只需求一次 的Moore-Penrose逆，因最多可存在K!种可能的配对情况，因此需进行K!次运算；当信源数K较大时，式(9)的运算量增加，进一步降维优化，若记T的第i行记为T_i， 的第i行记为 则

JMPMLS=minTi||Rsi′-TiR^s||F2---(10)]]>

T_i的解为e₁=[10…0]，e₂=[01…0]，……，e_K=[00…1]中的一个，且T每行的解不一样，因此只需计算(K-1)(K+2)/2次式(10)即可得出T；

步骤五：根据两组一维波达角的空间几何关系得出目标的方位角和俯仰角；目标的方位角θ_k和俯仰角

得出θ_k后根据cosα_k,cosβ_k的正负确定θ_k在四个象限的位置，调整θ_k大小。

现有技术中有的配对方法受传感器类型限制而适用范围有限，或者仅适用于均匀L阵和非相干源情况，并且鲁棒性不高；本发明的优势在于：第一，本发明的配对与一维波达角估计独立进行，能充分利用已有的比较成熟的一维线阵的解相干、信源数估计和波达角估计算法；第二，本发明在低信噪比和小快拍数条件下依然具有较高鲁棒性；第三，相干源和非均匀L阵条件下，该配对方法依然适用。大量的实验仿真结果表明，该发明具有很高实际应用价值。

附图说明

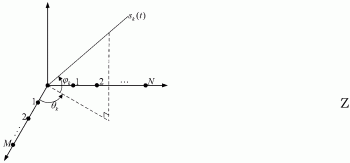
图1为L阵空间信号模型；

图2a SNR=5dB，未有效配对时目标俯仰-方位星座图；

图2b SNR=5dB，采用本发明配对后目标俯仰-方位星座图；

图3为本发明在独立源情况下配对成功率随信噪比的变化情况；

图4为本发明在相干源情况下配对成功率随信噪比的变化情况；

图5为本发明在SNR=-5dB时配对成功率随快拍数的变化情况；

图6为本发明在多目标情况下配对后所得目标俯仰角-方位角星座图。

具体实施方式

下面结合附图和实例，对本发明作更详细的说明。

L阵的信号模型

L阵由两个互相垂直的线阵构成，如图1所示。设两线阵X、Y相交于原点，阵元数分别为M+1、N+1，总阵元数为M+N+1。设有K个同中心频率的远场窄带信号被该L阵接收，λ为载频波长，θ_k和 分别表示第k个来波信号的方位角和俯仰角(θ∈[0,2π], )，假设信源在两个线阵上是可分的，此时将L阵的二维波达角估计问题可以分解为两个一维波达角估计。

记a_x,a_y为线阵X、Y的导向矢量，x_m为X轴上第m个阵元到原点的距离(m=1,2,…M)，y_n为Y轴上第n个阵元到原点的距离(n=1,2,…,N)，则信源k的导向矢量可以表示为

ax(αk)=[1,e-j2πx1λcosαk,e-j2πx2λcosαk,···,e-j2πxMλcosαk]Tk=1,2,···,Kay(βk)=[1,e-j2πy1λcosβk,e-j2πy2λcosβk,···,e-j2πyNλcosβk]Tk=1,2,···,K---(1)]]>

其中， 记A_x、A_y分别为线阵X和线阵Y的阵列流型，A_x(α)=[a_x(α₁),a_x(α₂),…,a_x(α_K)]，A_y(β)=[a_y(β₁),a_y(β₂),…,a_y(β_K)]。s_k为第k个信源的复包络，则回波信号可以表示为s(t)=[s₁(t),s₂(t),…,s_K(t)]^T。

记n_x,n_y为高斯白噪声，则X阵列和Y阵列的接收数据分别为

X(t)=Ax(α)s+nx=Σk=1Kax(αk)sk(t)+nx(t)Y(t)=Ay(β)s+ny=Σk=1Kay(βk)sk(t)+ny(t)---(2)]]>

配对过程

即分别估计出目标与线阵X、Y的夹角α,β，由于α_k,β_k是分别由线阵X、Y独立估计的，因此其顺序很难保证是一一对应的，配对的目的就是求出这种对应关系，然后由下式求出目标的方位角θ_k和俯仰角

得出θ_k后根据cosα_k,cosβ_k的正负确定θ_k在四个象限的位置，调整θ_k大小。

本发明提出PMLS算法，PMLS为Pair-matching method based on Maximum Likelihood using Source covariance matrix的缩写，实现两组一维波达角的配对。

在高斯白噪声背景下，本发明所估计的第一个信源协方差矩阵 的最大似然估计可以表示为

R^s=E{s^s^H}=E{A^y+·YYH·(A^yH)+}=A^y+Ryy(A^yH)+---(4)]]>

其中 为由线阵Y所估计的 构造的阵列流型， 中各角度的顺序任意， 为 的Moore-Penrose逆，R_yy为线阵Y接收数据的协方差矩阵

Ryy=E{YYH}=Ay·E{ssH}&CenterDo

一种L阵方位角和俯仰角配对的信号处理方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。