专利摘要

专利摘要

本发明公开了基于LSSVM的光伏最大功率点跟踪的控制方法，其步骤有：（1）建立光伏电池模型；（2）确定模型中设定温度值和太阳辐射强度下MPPT对应的电压和电流；（3）根据温度、太阳辐射强度、电压及电流的序列，得到最小二乘支持向量机模型中的训练集和测试集样本；（4）利用交叉验证方法选择最小二乘支持向量机的训练集的训练参数；（5）利用训练集的样本数据，通过选择的训练参数对最小二乘支持向量机进行训练，得到训练模型；（6）根据训练模型对所述测试集进行测试并对结果进行评价。本发明通过挖掘已知数据的内在规律，能够有效实现最大功率点处的输出电压和电流的跟踪，并且有效避免系统在最大功率点处震荡运行的缺点。

权利要求

1.一种基于LSSVM的光伏最大功率点跟踪的控制方法，其特征在于，所述方法包括如下步骤： 

（1）建立光伏电池模型； 

（2）确定模型中设定温度值和太阳辐射强度下MPPT对应的电压和电流； 

（3）根据温度、太阳辐射强度、电压及电流的序列，得到最小二乘支持向量机模型中的训练集和测试集样本； 

（4）利用交叉验证方法选择最小二乘支持向量机的训练集的训练参数； 

（5）利用训练集的样本数据，通过选择的所述训练参数对最小二乘支持向量机进行训练，得到训练模型； 

（6）根据所述训练模型对所述测试集进行测试并对结果进行评价。 

2.如权利要求1所述的控制方法，其特征在于，步骤（1）所述建立光伏电池模型是指根据光伏电池的工程数学模型，在MATLAB中建立其仿真模型。 

3.如权利要求1所述的控制方法，其特征在于，步骤（3）训练集和测试集样本的数据集为： 

其中， 

写成矩阵的形式即为： 

式中，x₁(n)为温度序列，x₂(n)为太阳辐射强度序列；y₁(n)为在最大功率点的输出电压序列，y₂(n)为在最大功率点的输出电流序列。 

4.如权利要求1所述的控制方法，其特征在于，步骤（4）所述训练参数包括正则化参数γ和核函数参数σ²；其核函数的表达式如下： 

。

5.如权利要求4所述的控制方法，其特征在于，步骤（4）所述利用交叉验证方法 选择最小二乘支持向量机的训练集的训练参数包括： 

将训练集分割成K个子集，其中一个子集被保留作为验证模型的数据，其他K-1个子集用来训练，交叉验证重复K次，每个子集验证一次； 

在训练前，给定正则化参数γ和核函数参数σ²的范围，即γ∈[γ_min,γ_max]，σ²∈[σ²_min,σ²_max]，使γ和σ²在这个范围内遍历取值，对每一个组合参数（γ，σ²）均进行10次交叉验证； 

选取均方误差MSE作为评价指标，将这10次测试结果的MSE取平均值作为该参数对应的指标，最后选择指标最高的一组参数组合作为最终的最优参数。 

6.如权利要求5所述的控制方法，其特征在于，步骤（5）是根据最优参数建立训练模型。 

说明书

技术领域

本发明属于光伏发电领域，具体涉及一种基于LSSVM的光伏最大功率点跟踪的控制方法。

背景技术

随着社会的快速发展，能源危机和环境污染成为亟待解决的问题。可再生能源的利用成为近年来各个领域研究的热点。太阳能具有普遍的存在性、储量的无限性、使用的清洁性等优点，是人类社会很理想的未来能源。利用太阳能进行发电是可持续发展能源战略的重要决策。

为了实现光能的最大利用率，需要对光伏电池进行最大功率点跟踪。目前，常用的实现最大功率点跟踪的方法主要有以下几种：恒定电压法、扰动观察法、电导增量法、最优梯度法、神经网络法等。其中，恒定电压法在温度变化不大时具有良好的可靠性和稳定性，但实际中，一年四季或每天晨午温差较大，该方法会降低系统运行效率。扰动观察法结构简单，测量参数少。电导增量法在外界温度和光照等环境发生变化时，其动态特性和跟踪特性较好。但扰动观察法和电导增量法由于步长固定，都存在一个缺点，即步长过小，则导致光伏电池长时间停留在低功率工作状态；如果步长过大，则导致光伏发电系统输出振荡加剧。针对此缺点，有学者提出变步长方法，当离最大功率点较远时，采用较大步长，加快寻优速度；当离最大功率点较近时，采用较小步长，保证跟踪精度，利于系统稳定。最优梯度法是一种以梯度法为基础的多维无约束最优化问题的数值计算法，该方法中需要选择电压增量系数，相当于扰动观察法和电导增量法中的步长。神经网络具有大规模并行处理能力、容错性、自组织及自适应能力强等特点，但也有易陷入局部最小、神经网络结点个数难以确定等不可避免的缺点。

发明内容

针对现有技术的不足，本发明提出一种基于MATLAB/Simulink中LSSVM工具箱的光伏最大功率点跟踪的控制方法，能够有效避免系统在最大功率点处震荡运行。

本发明提供的一种基于LSSVM的光伏最大功率点跟踪的控制方法，其改进之处在于，所述方法包括如下步骤：

（1）建立光伏电池模型；

（2）确定模型中设定温度值和太阳辐射强度下MPPT对应的电压和电流；

（3）根据温度、太阳辐射强度、电压及电流序列，得到最小二乘支持向量机模型中的训练集和测试集样本；

（4）利用交叉验证方法选择最小二乘支持向量机的训练集的训练参数；

（5）利用训练集的样本数据，通过选择的所述训练参数对最小二乘支持向量机进行训练，并根据最优参数得到训练模型；

（6）根据所述训练模型对所述测试集进行测试并对结果进行评价。

其中，步骤（1）所述建立光伏电池模型是指根据光伏电池的工程数学模型，在MATLAB中建立其仿真模型。

其中，步骤（3）训练集和测试集样本的数据集为：

D‾={X(n),Y(n)},n=1,2,···,M---1)]]>

其中，

X(n)=[x1(n),x2(n)],n=1,2,···MY(n)=[y1(n),y2(n)],n=1,2,···M---2)]]>

写成矩阵的形式即为：

X=x1(1)x2(1)x1(2)x2(2)······x1(M)x2(M),Y=y1(1)y2(1)y1(2)y2(2)······y1(M)y2(M)---3)]]>

式中，x₁(n)为温度序列，x₂(n)为太阳辐射强度序列；y₁(n)为在最大功率点的输出电压序列，y₂(n)为在最大功率点的输出电流序列。

其中，步骤（4）所述训练参数包括正则化参数γ和核函数参数σ²；其核函数的表达式如下：

其中，步骤（4）所述利用交叉验证方法选择最小二乘支持向量机的训练集的训练参数包括：

将训练集分割成K个子集，其中一个子集被保留作为验证模型的数据，其他K-1个子集用来训练，交叉验证重复K次，每个子集验证一次；

在训练前，给定正则化参数γ和核函数参数σ²的范围，即γ∈[γ_min,γ_max]，σ²∈[σ²_min,σ²_max]，使γ和σ²在这个范围内遍历取值，对每一个组合参数（γ，σ²）均进行10次交叉验证；

选取均方误差MSE（Mean Square Error）作为评价指标，将这10次测试结果的MSE取平均值作为该参数对应的指标，最后选择指标最高的一组参数组合作为最终的最优参数。

与现有技术比，本发明的有益效果为：

（1）本发明通过挖掘已知数据的内在规律，能够有效实现最大功率点处的输出电压和电流的跟踪。

（2）本发明能够有效避免系统在最大功率点处震荡运行的缺点。

（3）本发明能够避免算法中有步长时的缺点，即步长过小，则导致光伏电池长时间停留在低功率工作状态；如果步长过大，则导致光伏发电系统输出振荡加剧。

（4）本发明是一种基于结构风险最小化的学习算法，既有严格的理论基础，又能较好地解决过学习、欠学习、非线性、高维数和局部最优等问题。

（5）本发明通过选择支持向量机进行计算，是一种新的思路，为以后的理论知识提供基础。

附图说明

图1为本发明提供的光伏电池I-V特性曲线示意图。

图2为本发明提供的光伏电池P-V特性曲线示意图。

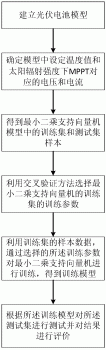
图3为本发明提供的利用LSSVM实现MPPT的流程图。

图4为本发明提供的测试集仿真结果示意图。

图5为本发明提供的测试集仿真结果误差示意图。

图6为本发明提供的测试集仿真结果相对误差示意图。

具体实施方式

下面结合附图对本发明的具体实施方式作进一步的详细说明。

本实施例提供的一种基于LSSVM的光伏最大功率点跟踪的控制方法，其流程图如图3所示，具体包括如下步骤：

步骤（1），在MATLAB仿真软件中建立光伏电池模型。根据光伏电池的工程数学模型，在MATLAB中建立其仿真模型，本实施例中，设置光伏电池的参数如下：V_oc＝42V，I_sc＝4.5A，V_m＝34V，I_m＝4A，T_ref＝25°C，S_ref＝1kW/m²。该模型输出特性曲线的仿真结果如图1和图2所示。

步骤（2），根据步骤（1）中所述的光伏电池模型，得到某些温度和太阳辐射强度下MPPT对应的电压和电流。分别将温度在0～40°C之间、太阳辐射强度在0～4kW/m²之间间隔取值，经过仿真分析得到对应温度和太阳辐射强度条件下的最大功率点输出电压和电流。

步骤（3），根据步骤（2）中所述的电压和电流序列，得到最小二乘支持向量机模型中的训练集和测试集样本。

得到的数据集为

D‾={X(n),Y(n)},n=1,2,···,M---(1)]]>

其中，

X(n)=[x1(n),x2(n)],n=1,2,···MY(n)=[y1(n),y2(n)],n=1,2,···M---(2)]]>

写成矩阵的形式即为：

X=x1(1)x2(1)x1(2)x2(2)······x1(M)x2(M),Y=y1(1)y2(1)y1(2)y2(2)······y1(M)y2(M)---(3)]]>

式中，x₁(n)为温度序列，x₂(n)为太阳辐射强度序列；y₁(n)为在最大功率点的输出电压序列，y₂(n)为在最大功率点的输出电流序列。

具体样本数据如表1和表2所示。

表1训练集数据

表2测试集数据

根据已知某些典型温度和太阳辐射强度条件下的最大功率点以及工作在最大功率点处的输出电压和输出电流，可以找到一个映射函数，使得

Y(n)＝F(X(n))    （4）

最小二乘支持向量是在标准支持向量机的基础上发展而来的，它将标准支持向量机中约束条件中的不等式约束变为等式约束，从而使求解二次规划问题转化为求解一组线性方程问题回归模型的优化问题。描述如下：

设决策函数为y＝(ω·x)+b，最优化问题变为：

minω,b12||ω||2+γ2Σi=1lξi2s.t.yi=(ω·xi)+b+ξi,i=1,···,l---(5)]]>

引入Lagrange函数

L(ω,b,ξ,α)=12||ω||2+γ2Σi=1lξi2-Σi=1lαi((ω·xi)+b+ξi-yi)---(6)]]>

根据KKT条件，最优化条件变为：

∂L∂ω=0→ω=Σi=1lαixi]]>

∂L∂b=0→Σi=1lαi=0]]>    （7）

∂L∂ξi=0→αi=γξii=1,···,l]]>

∂L∂αi=0→(ω·xi)+b+ξi-yi=0i=1,···,l]]>

写成矩阵形式并消去ω和ξ，化简得到

01T1XTX+γ-1Ibα=0Y---(8)]]>

求解此线性方程组就可以求得决策函数。对于非线性回归问题，引入核函数方法来求解即可。选用RBF核函数，如式（9）所示。故最小二乘支持向量机预测模型中有两个参数需要选择，即正则化参数γ和核函数参数σ²。

步骤（4），利用交叉验证方法对最小二乘支持向量机的训练参数进行选择。

K折交叉验证方法的思路如下：将训练集分割成K个子集，K一般大于等于2，其中一个子集被保留作为验证模型的数据，其他K-1个子集用来训练。交叉验证重复K次，每个子集验证一次。在训练前，给定正则化参数γ和核函数参数σ²的范围，即γ∈[γ_min,γ_max]，σ²∈[σ²_min,σ²_max]，使γ和σ²在这个范围内遍历取值，对每一个组合参数（γ，σ²）均进行10次交叉验证（K=10）。选取均方误差MSE（Mean Square Error）作为评价指标，将这10次测试结果的MSE取平均值作为该参数对应的指标，最后选择指标最高（即MSE最小）的一组参数组合作为最终的最优参数。

步骤（5），利用训练集样本数据，采用步骤（4）中所述方法选择到的参数对最小二乘支持向量机进行训练，得到训练模型。

步骤（6），利用得到的训练模型，对测试集进行测试并对结果进行评价。测试集仿真结果如图4所示，图中，方形符号代表在MPP处的电压、电流值，星形符号代表该方法控制下输出的电压、电流值；测试集仿真结果误差如图5所示，图中，方形符号代表仿真结果中电压的误差，星形符号代表仿真结果中电流的误差；测试集仿真结果相对误差如图6所示，图中，方形符号代表仿真结果中电压的相对误差，星形符号代表仿真结果中电流的相对误差。

根据图5、图6的仿真结果，MPP处的输出电压仿真结果的相对误差最大值为3.2%，绝大部分结果相对误差小于1%。MPP处的输出电流仿真结果的相对误差最大值为1%，绝大部分结果相对误差小于0.5%。可见，利用LSSVM实现MPPT的方法，能够较准确地实现最大功率点处的输出电压和电流的跟踪。本发明能够有效避免系统在最大功率点处震荡运行的缺点。

利用LSSVM方法仿真得到的电压或者电流值，可以应用到光伏发电系统后续的控制电路中。

最后应当说明的是：以上实施例仅用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员应当理解：依然可以对本发明的具体实施方式进行修改或者等同替换，而未脱离本发明精神和范围的任何修改或者等同替换，其均应涵盖在本发明的权利要求范围当中。

一种基于LSSVM的光伏最大功率点跟踪的控制方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。