专利摘要

专利摘要

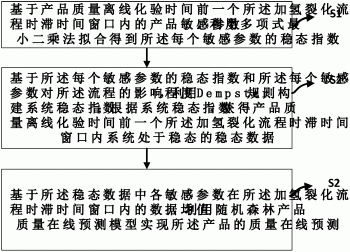
本发明提供一种加氢裂化流程产品质量在线预测方法。所述方法包括：S1基于产品质量离线化验时间前一个流程时滞时间窗口内的产品的敏感参数，利用多项式最小二乘法拟合得到所述每个敏感参数的稳态指数；S2基于所述每个敏感参数的稳态指数和所述每个敏感参数对所述流程的影响程度，利用Dempster规则构建系统稳态指数；根据系统稳态指数，获得产品质量离线化验时间前一个流程时滞时间窗口内系统处于稳态的稳态数据；S3基于所述稳态数据中各敏感参数在流程时滞时间窗口内的数据均值，利用随机森林产品质量在线预测模型实现所述产品的质量在线预测。本发明的方法充分利用加氢裂化全流程过程变量使得预测得到的质量能够反映全局运行状况。

权利要求

1.一种加氢裂化流程产品质量在线预测方法，其特征在于，包括：

S1.基于产品质量离线化验时间前一个所述加氢裂化流程时滞时间窗口内的产品敏感参数，利用多项式最小二乘法拟合得到所述每个敏感参数的稳态指数；

S2.基于所述每个敏感参数的稳态指数和所述每个敏感参数对所述流程的影响程度，利用Dempster规则构建系统稳态指数；根据系统稳态指数，获得产品质量离线化验时间前一个所述加氢裂化流程时滞时间窗口内系统处于稳态的稳态数据；

S3.基于所述稳态数据中各敏感参数在所述加氢裂化流程时滞时间窗口内的数据均值，利用随机森林产品质量在线预测模型实现所述产品的质量在线预测。

2.根据权利要求1所述的方法，其特征在于，S1中利用多项式最小二乘法拟合得到所述每个敏感参数的稳态指数具体为：

使用多项式最小二乘法拟合对每个所述敏感参数的采样区间数据进行滑动窗口回归，得到敏感参数在各个采样点的回归值；

使用多项式最小二乘法拟合所述敏感参数的回归值的变化信息，得到所述敏感参数的稳态指数。

3.根据权利要求1或2所述的方法，其特征在于，所述产品敏感参数的获取包括：

从生产数据库中提取加氢裂化全流程中相关的过程变量；

基于所述过程变量在外部条件发生变化时的波动趋势，筛选出主要过程变量；

使用带滑窗的中值滤波对所述主要过程变量的实际历史运行数据进行滤波去噪得到所述敏感参数。

4.根据权利要求3所述的方法，其特征在于，所述敏感参数的获取还包括：

在去噪后，基于滤波去噪后的主要过程变量，利用Spearman相关性分析的部分逐步回归法定义敏感变量因子并进行敏感变量优选，得到所述敏感参数。

5.根据权利要求1或2所述的方法，其特征在于，在使用多项式最小二乘法之前还包括将所述敏感参数经过PCA归一化和正规化特征向量矩阵变化处理。

6.根据权利要求5所述的方法，其特征在于，所述PCA主成分分析法归一化处理包括：

基于所述敏感参数，利用主成分分析法归一化得到主成分，所述主成分为敏感参数，并将每个敏感参数的单个贡献率定义为稳态权重因子。

7.根据权利要求1所述的方法，其特征在于，S2中Dempster规则构建系统稳态指数的公式为：

$SSSI\left(t\right)=\underset{i=1}{\overset{n}{\Pi }}{\left[{\mathrm{SSI}}_i\left(t\right)\right]}^{{\mathrm{SSWF}}_i/{\mathrm{\Sigma SSWF}}_i}$

其中，SSSI表示系统稳态指数，SSI和SSWF分别指的是各敏感参数的稳态指数和稳态权重因子，i为敏感参数序号。

8.根据权利要求1所述的方法，其特征在于，S3中随机森林产品质量在线预测模型的构建为：

基于炼油工厂数据库中的敏感参数，遍历S1和S2，得到稳态数据；

将所述稳态数据中各敏感参数在所述流程时滞时间窗口内的数据均值作为所述敏感参数的特征值，与该离线化验时间的产品质量组成训练集的一个样本元素；

使用随机森林回归算法训练所建立的训练集，构建所述模型。

9.根据权利要求8所述的方法，其特征在于，所述随机森林回归算法具体为：

S31.假定RF算法中需建立的决策树数量为k，对于每棵决策树，采用自助法重采样方法有放回地从总训练集T中随机抽取和T样本容量相同的训练集T_i(i＝1,…,k)，并分别作为k棵决策树的训练集；

S32.对于第i棵决策树的每个分支节点，采用不放回的采样方法从所述敏感参数特征集M中随机抽取m个特征变量作为特征子集M_ij(i＝1,…,k,j＝1,2,…)，j表示该决策树使用特征子集的个数；每个分支节点的特征子集M_ij的特征变量数m为总特征变量M维度的开方，即 则

S33.对每棵决策树，以T_i为训练样本，M_i为特征子集集合进行训练，从M_ij中选择一个最具有分类能力的变量对该节点进行分裂，得到一个随机森林回归模型{RF(T_i,M_i),i＝1,…,k,}，其中，RF(T_i,M_i)为每棵决策树分类结果；

S34.输入敏感参数特征值向量X，通过收集各个决策树的预测值，并对其加权均值作为产品质量预测结果，即：

$Q=f\left(X\right)=\frac{1}{k}{\Sigma }_{i=1}^k{\mathrm{RF}}_i\left(X\right).$

说明书

技术领域

本发明涉及产品质量检测领域，更具体地，涉及一种加氢裂化流程产品质量在线预测方法。

背景技术

加氢裂化流程是石化企业极为重要的一个二次加工工艺流程，即在加热、高氢压和催化剂的条件下，使重质油发生裂化反应，转化成石脑油、汽油、航煤、柴油等轻质、高质量的油品。加氢裂化流程具有加工原料范围宽、原料适应性强、生产灵活性大、碳丢失率低、产品质量好、液体产品收率高等优点，是大型炼厂和石化企业最重要、最可靠、最灵活和最有效的加工手段之一，并且其产品也被广泛用于汽车、航空、船舶、重型机械、润滑油生产等方面。

然而，由于原料油属性变化、催化剂活性降低、装置性能退化、生产方案及操作参数变化等原因，加氢裂化流程产品质量也在发生变化，并且，产品的质量不仅代表该流程的运行状况好坏，也会对下游的石化流程起到至关重要的作用。因此，对加氢裂化流程产品质量进行检测并根据产品质量对过程进行评估、调整尤为重要。

目前，实际的加氢裂化流程产品质量检测大都采用人工离线化验，这种检测方式存在严重滞后，很可能导致操作人员不能及时调整过程变量而生产出不合格的产品油。为了及时评估加氢裂化流程的全局运行状况、并做出相应的调整，在线的产品质量检测则显得尤为关键。然而，考虑到安全性和可操作性，像馏点、硫含量、闪点、水含量等产品质量指标是无法通过在线化验方式进行检测的。因此，使用软测量技术来实现加氢裂化流程产品质量在线预测成为了学者们研究的热点问题。

软测量技术是以可测或易测的过程变量(或辅助变量)为基础，利用辅助变量和难测或待测过程变量(或主导变量)之间的数学关系(即软测量模型)，通过各种数学计算和估计实现对主导变量的测量。广义的软测量技术其实主要由数据采集、数据处理、软测量模型和软测量数据存储、显示与输出4个部分组成。

目前，根据软测量模型建立的方式，加氢裂化流程产品质量在线预测方法分为基于机理的和数据驱动的两种。基于机理的加氢裂化流程产品质量在线预测是建立在对加氢裂化流程工艺和机理有深刻认识的基础上，通过对加氢裂化流程产品质量的机理分析，找出其他实时可测辅助变量和不可测产品质量指标之间的关系，例如结合主要的过程变量和轻石脑油干点的关联公式，建立加氢裂化流程产品质量在线预测模型。但这种方法只能适用于机理明确的化工过程，并且针对每种产品质量指标都需要建立特定的模型，建模过程复杂。

基于数据驱动的加氢裂化流程产品质量在线预测是通过多元线性回归(MLR)、主元分析(PCR)、部分最小二乘(PLS)等统计分析方法和人工神经网络(ANN)、模糊技术、支持向量机(SVM)等智能算法，利用实际加氢裂化流程生产数据建立实时可测辅助变量和不可测产品质量指标之间的回归模型，从而实现产品质量的在线预测。这种方法非常适合变量多、非线性的复杂系统，泛化性能好，简单实用，具有较高的应用价值。然而，目前来说，该类方法研究仍存在以下问题：第一，并没有充分利用加氢裂化全流程过程变量，所建立的产品质量在线预测模型基本都是只考虑分馏系统这一部分的过程变量，不利于加氢裂化流程全局运行状况评估；第二，加氢裂化流程过程变量多，目前主要依靠机理分析和工厂经验选取辅助变量，主观因素大；第三，加氢裂化流程是个大时滞系统，即使是分馏系统也有近1.5小时的时滞，在外部条件发生变化时，该过程存在稳态和非稳态情况，不同模态下所建立的质量在线预测模型也是不同的，需要区分。

发明内容

本发明针对现有加氢裂化产品质量预测的数据驱动建模存在的问题，提供一种加氢裂化流程产品质量在线预测方法，所述方法包括：

S1.基于产品质量离线化验时间前一个所述加氢裂化流程时滞时间窗口内的产品敏感参数，利用多项式最小二乘法拟合得到所述每个敏感参数的稳态指数；

S2.基于所述每个敏感参数的稳态指数和所述每个敏感参数对所述流程的影响程度，利用Dempster规则构建系统稳态指数；根据系统稳态指数，获得产品质量离线化验时间前一个所述加氢裂化流程时滞时间窗口内系统处于稳态的稳态数据；

S3.基于所述稳态数据中各敏感参数在所述加氢裂化流程时滞时间窗口内的数据均值，利用随机森林产品质量在线预测模型实现所述产品的质量在线预测。

与现有的方法相比，本发明提出的加氢裂化流程产品质量在线预测方法具有以下效果：

充分利用加氢裂化全流程过程变量使得预测得到的质量能够反映全局运行状况；基于Spearman相关分析的部分逐步回归法引入了敏感变量因子SVF，从多类型、多分布和多关联海量数据中提取反映当前运行状况、与产品质量密切相关的敏感变量；基于主成分分析(PCA)对敏感变量进行降维，得到敏感参数，对高维的特征进行降维、降低计算复杂度、加快处理速度，而且它还可以处理高耦合性特征，以使敏感参数尽量互不相关从而完全表现出系统的特征；基于主成分分析(PCA)中的单个主元贡献率引入了稳态权重因子SSWF，从而消除了以往在构建系统稳态指数SSSI时采用经验赋值的主观因素影响；充分考虑系统的稳态和非稳态的情况，基于稳态数据建立加氢裂化流程柴油产品质量在线预测模型，科学严谨；使用的随机森林回归算法(RFR)相对于其他机器学习算法来说，具有预测精度高、泛化能力好、收敛速度快等优点，可有效避免“过拟合”现象的发生，适合各种高维数据集。

附图说明

图1为根据本发明实施例中加氢裂化流程产品质量在线预测方法的总体流程图；

图2为根据本发明一个优选实施例中加氢裂化流程产品质量在线预测方法的总体流程图；

图3为根据本发明实施例1中基于主成分分析法的敏感参数及其稳态权重因子获取的流程图；

图4为根据本发明实施例1中多项式最小二乘法拟合对敏感参数的采样区间数据进行滑动窗口回归示意图；

图5为根据本发明实施例1中随机森林回归算法单棵决策树算法简图；

图6为根据本发明实施例1中随机森林回归算法简图。

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

本发明的加氢裂化流程产品质量在线预测方法，包括：

S1.基于产品质量离线化验时间前一个所述加氢裂化流程时滞时间窗口内的产品敏感参数，利用多项式最小二乘法拟合得到所述每个敏感参数的稳态指数；

S2.基于所述每个敏感参数的稳态指数和所述每个敏感参数对所述流程的影响程度，利用Dempster规则构建系统稳态指数；根据系统稳态指数，获得产品质量离线化验时间前一个所述加氢裂化流程时滞时间窗口内系统处于稳态的稳态数据；

S3.基于所述稳态数据中各敏感参数在所述加氢裂化流程时滞时间窗口内的数据均值，利用随机森林产品质量在线预测模型实现所述产品的质量在线预测。

本发明的方法充分利用加氢裂化全流程过程变量，使得预测得到的质量能够反映全局运行状况。

在本发明的一个实施例中，为了更好的去噪，在S1中使用多项式最小二乘法拟合对每个所述敏感参数的采样区间数据进行滑动窗口H回归，得到敏感参数在各个采样点的回归值，用回归值代替原测量值可以更好地去噪。

同时，多项式最小二乘法拟合含有所述敏感参数的回归值的变化信息，求一阶导，得到敏感参数的稳态指数。即多项式最小二乘法拟合含有敏感参数的变化信息，其在采样点的一阶导数即为该敏感参数在该采样点的变化快慢，并将共定义为该敏感参数的稳态指数SSI，根据敏感参数的稳态指数可以检测该敏感参数信号的稳态和非稳态。

在一个优选实施例中，多项式最小二乘法拟合的具体步骤为：

对某个敏感参数在采样区间的序列x(j)进行多项式最小二乘法拟合时，首先定义一个长度为奇数的H长窗口，H＝2h+1，h为正整数。设在某一时刻，窗口内的信号样本为x(j-h),…,x(j),…,x(j+h)，其中x(j)为位于窗口中心的该敏感参数样本值。

令窗口内的信号样本x(j-h),…,x(j),…,x(j+h)为x′(1),…,x′(h+1),…,x′(2h+1)，其中x′(h+1)为位于窗口中心的该敏感参数样本值，对应的采样时刻t分别为1,2…,2h+1，则窗口内的拟合信号 则可以表示为时间t的函数，即：

其中，a＝[a₀a₁,…,a_n]^T,n<2h+1为多项式最小二乘法拟合模型参数向量，r(t)＝[1,t,t²,…,tⁿ]^T为回归变量。应用最小二乘法就可以得到参数a的最优估计：

式中：

则经过多项式最小二乘法拟合后的拟合信号为

则敏感参数在各个采样点x(j)的回归值为：

用回归值代替原测量值可以去噪。采用滑动窗口方法即可得到该敏感参数在采样区间的多项式最小二乘法拟合回归值序列。

在一个优选实施例中，为了减少随外部条件变化而波动变化不大的相关变量以及波动无规则的相关变量，本发明方法中敏感参数的获取包括以下步骤：

1)从生产数据库中提取加氢裂化全流程中过程变量；

2)基于所述过程变量在外部条件发生变化时的波动趋势，筛选出主要过程变量；

3)使用带滑窗的中值滤波对所述主要过程变量的实际历史运行数据进行滤波去噪，得到所述敏感参数。

在所述步骤1)中，从炼油工厂数据库中提取加氢裂化全流程可测过程变量及其历史数据，根据工艺和机理，初步提取与产品质量相关过程变量。

在所述步骤2)中，分析当外部条件发生变化时各个相关变量的趋势波动情况，筛选出主要过程变量。目的是为了排除无波动、平稳的相关变量，即随外部条件变化而波动变化不大的相关变量，并排除波动无规则的相关变量，即与外部条件变化无关的变化剧烈的相关变量。

在所述步骤3)中，采用滑动窗口为L的中值滤波对主要变量的实际历史运行数据进行滤波去噪，从而消除加氢裂化流程仪表检测时、数据传输过程中受到的干扰。

其中，所述步骤3)中采用滑动窗口为L的中值滤波的具体步骤为本领域中常用的中值滤波法，在本发明的方法中优选的步骤为：

对某个主要变量在采样区间的序列x(j)进行滤波处理时，首先定义一个长度为奇数的L长窗口，L＝2N+1，N为正整数。设在某一时刻，窗口内的信号样本为

x(j-N),…,x(j),…,x(j+N)

其中，x(j)为位于窗口中心的该主要变量样本值。

对L个该主要变量样本值按从小到大的顺序排列后，其中排序在j处的样本值便定义为中值滤波的输出值，表达式为：

y(j)＝Med[x(j-N),…,x(j),…,x(j+N)]

采用滑动窗口方法即可得到该主要变量在采样区间的中值滤波序列。

为了减少选取变量的冗余信息，大大降低计算量，所述敏感参数的获取还包括：

在去噪后，基于滤波去噪后的主要过程变量，利用Spearman相关性分析的部分逐步回归法定义敏感变量因子并进行敏感变量优选，得到所述敏感参数。

即根据外部变化的条件(如进料总流量)与主要过程变量的Spearman相关性系数，定义敏感变量因子SVF，设定阈值为ε∈[0,1]，筛选出敏感变量因子大于ε的主要过程变量，得到敏感变量，并部分逐步引入非敏感变量或剔除敏感变量，根据预测偏差Δe来验证所选取的敏感变量正确性。

在本发明的一个实施例中，利用Spearman相关系统确定敏感变量因子，并结合逐步回归法的优点来验证筛选出的敏感变量是否正确。

其中，基于Spearman相关性分析的部分逐步回归法的具体步骤包括：

根据Spearman相关性系数分析外部变化的条件(如原料总入口流量)与主要过程变量的相关性，计算公式为：

K为主要变量个数，x₁为加氢裂化流程进料泵出口流量的采样数据，x_i为其他主要变量的采样数据。

定义第i变量的敏感变量因子为：SVF_i＝ρ_i，设定阈值为ε∈[0,1]，筛选出敏感变量因子大于ε的主要过程变量，得到敏感变量。并部分逐步引入非敏感变量或剔除敏感变量，根据预测偏差Δe来验证所选取的敏感变量正确性，判别公式为：

Δe＝e′-e≤(0.05～0.1)e

e为所选取的敏感变量时的预测结果，e′为在敏感变量的基础上引入或剔除变量时的预测结果。

在一个优选实施例中，为了对高维的特征进行降维、降低计算复杂度、加快处理速度，在使用多项式最小二乘法之前还包括将所述敏感参数经过PCA归一化和正规化特征向量矩阵变化处理。

其中，基于主成分分析法(PCA)对敏感参数进行降维，当前n个成分累计贡献大于或等于ξ时，取其为主成分并将其作为降维后敏感参数，并将每个敏感参数的单个贡献率(或相关系数矩阵特征值)定义为稳态权重因子SSWF，稳态权重因子是指每个敏感参数对多变量系统的影响程度。

使用PCA的目的是其不仅可以对高维的特征进行降维、降低计算复杂度、加快处理速度，而且它还可以处理高耦合性特征，以使敏感参数尽量互不相关从而完全表现出系统的特征。

所述基于主成分分析法的敏感参数获取的具体步骤包括：

1)对敏感变量的采样数据进行归一化：

由于不同敏感变量的量纲不同，为了处理方便，应先对原始数据进行归一化，记敏感变量的采样数据中共有M个样本，每个样本有N个敏感变量，则共有N个敏感变量向量，分别记为C_i(i＝1,2,…,N)，而C_ji(j＝1,2,…,M；i＝1,2,…,N)为第j样本的第i个敏感变量样本值。

归一化计算公式为：

其中，E(C_i)指C_i的均值，Var(C_i)指C_i的标准差。

2)求敏感变量间的相关系数矩阵：

经过归一化后的敏感变量向量为G_i(i＝1,2,…,N)，N个敏感变量的相关系数可以构成一个N×N的相关系数矩阵R，R中的每个元素记为R_ij(i＝1,2,…,N；j＝1,2,…,N)，每个元素的值为：

式中Conv(G_i,G_j)表示G_i和G_j的协方差，D(G_i)和D(G_j)分别表示G_i和G_j的方差。可以发现相关系数矩阵R是个对称矩阵。

3)求敏感变量正规化单位特征向量。对于N×N的相关系数矩阵R，共可求得N个特征值，记为λ_i，根据由大到小依次排序为λ₁、λ₂、…、λ_N，再求出每个特征值所对应的正规化单位特征向量，记为L_i＝[l_1i l_2i…l_Ni]^T。

4)根据特征值的累计贡献率确定主成分，即敏感参数。

累计贡献率是由特征值的大小所决定的，则前n成分的累计贡献率CR_n计算公式如下：

当累计贡献率CR_n≥ξ，其中ξ为控制值，这时的n为敏感参数个数，新的敏感参数正规化单位特征向量矩阵为步骤3)中前n个正规化单位特征向量L₁、L₂、…、L_n组成的矩阵L′，新的敏感参数的样本数据矩阵为Y＝D×L′，新的敏感参数即为Y的列属性。

其中，敏感参数稳态权重因子SSWF为敏感参数的单个贡献率(或相关系数矩阵特征值)，即每个敏感参数稳态权重因子为：

它反映每个敏感参数对多变量系统的影响程度。

在本发明一个优选实施例中，S2中基于所述每个敏感参数的稳态指数和所述每个敏感参数对所述流程的影响程度，利用Dempster规则构建系统稳态指数；其中，所述每个敏感参数对所述系统的影响程度也称稳态权重因子，可以为当敏感参数经过主成分分析法后进行降维处理时每个敏感参数的单个贡献率，也可以用其它方法测定。

其中，S2中Dempster规则构建系统稳态指数的公式为：

其中，SSSI表示系统稳态指数，SSI和SSWF分别指的是各敏感参数的稳态指数和稳态权重因子，i为敏感参数序号。

设定阈值μ，根据检测精度来取值，一般取值为0.6～1，从而判断加氢裂化流程系统是否处于稳态，其中，当SSSI大于阈值μ，则认为系统瞬时稳态。

在本发明一个优选实施例中，S3中随机森林产品质量在线预测模型的构建为：

基于炼油工厂数据库中的敏感参数，遍历S1和S2，得到稳态数据；

将所述稳态数据中各敏感参数在所述流程时滞时间窗口内的数据均值作为所述敏感参数的特征值，与该离线化验时间的产品质量组成训练集的一个样本元素；

使用随机森林回归算法训练所建立的训练集，构建所述模型

在一个优选实施例中，所述随机森林回归算法具体为：

S31.假定RF算法中需建立的决策树数量为k，对于每棵决策树，采用自助法重采样方法有放回地从总训练集T中随机抽取和T样本容量相同的训练集T_i(i＝1,…,k)，并分别作为k棵决策树的训练集；

S32.对于第i棵决策树的每个分支节点，采用不放回的采样方法从所述敏感参数特征集M中随机抽取m个特征变量作为特征子集M_ij(i＝1,…,k,j＝1,2,…)，j表示该决策树使用特征子集的个数；每个分支节点的特征子集M_ij的特征变量数m为总特征变量M维度的开方，即 则

S33.对每棵决策树，以T_i为训练样本，M_i为特征子集集合进行训练，从M_ij中选择一个最具有分类能力的变量对该节点进行分裂，得到一个随机森林回归模型{RF(T_i,M_i),i＝1,…,k,}，其中，RF(T_i,M_i)为每棵决策树分类结果；

S34.输入敏感参数特征值向量X，通过收集各个决策树的预测值，并对其加权均值作为产品质量预测结果，即：

实施例1：

一种加氢裂化流程柴油产品质量在线预测方法，流程图如图2所示，包括以下步骤：

步骤(1)、从炼油工厂数据库中提取1700多个加氢裂化全流程可测过程变量及其历史数据，根据工艺和机理，初步提取与柴油产品质量相关的162个过程变量；

步骤(2)、分析当加氢裂化流程进料总流量发生变化时，各个相关变量的趋势波动情况，筛选出68个主要过程变量。目的是为了排除无波动、平稳的相关变量，即随进料总流量变化而波动变化不大的相关变量，并排除波动无规则的相关变量，即与进料总流量变化无关的变化剧烈的相关变量。

步骤(3)、采用滑动窗口为L＝215(加氢裂化流程的时滞)的中值滤波对主要变量的实际历史运行数据进行滤波去噪，从而消除加氢裂化流程仪表检测时、数据在传输过程中受到的干扰。其中滑动窗口为L＝215的中值滤波的具体步骤包括：对某个主要变量在采样区间的序列x(j)进行滤波处理时，首先定义一个长度为奇数的L长窗口，L＝2N+1，N为正整数。设在某一时刻，窗口内的信号样本为x(j-N),…,x(j),…,x(j+N)，其中x(j)为位于窗口中心的该主要变量样本值。对L个该主要变量样本值按从小到大的顺序排列后，其中排序在j处的样本值便定义为中值滤波的输出值，表达式为：

y(j)＝Med[x(j-N),…,x(j),…,x(j+N)]

采用滑动窗口方法即可得到该主要变量在采样区间的中值滤波序列。

步骤(4)、提出基于Spearman相关性分析的部分逐步回归法定义敏感变量因子SVF并进行敏感变量优选，即根据进料总流量与主要过程变量的Spearman相关性系数，计算公式为：

K为主要变量个数，x₁为加氢裂化流程进料泵出口流量的采样数据，x_i为其他主要变量的采样数据，定义第i变量的敏感变量因子为：SVF_i＝ρ_i，设定阈值为ε＝0.6，筛选出敏感变量因子大于ε的主要过程变量，得到42个敏感变量(如表1所示)，并部分逐步引入非敏感变量或剔除敏感变量，根据预测偏差Δe来验证所选取的敏感变量正确性，判别公式为：

Δe＝e′-e≤(0.05～0.1)e

e为所选取的敏感变量时的预测结果，e′为在敏感变量的基础上引入或剔除变量时的预测结果。目的是减少选取变量的冗余信息，并大大降低计算量。

表1本实施例基于敏感变量因子筛选出的敏感变量列表

步骤(5)、基于主成分分析法(PCA)对敏感变量进行降维，当前n个成分累计贡献大于或等于ξ＝95％时，取其为主成分(下面称为敏感参数)，并将每个敏感参数的单个贡献率(或相关系数矩阵特征值)定义为稳态权重因子SSWF，即每个敏感参数对多变量系统的影响程度。使用PCA的目的是其不仅可以对高维的特征进行降维、降低计算复杂度、加快处理速度，而且它还可以处理高耦合性特征，以使敏感参数尽量互不相关从而完全表现出系统的特征。其中基于主元分析法(PCA)(如图3所示)的敏感参数获取的具体步骤包括：

1)对敏感变量的采样数据进行归一化。由于不同敏感变量的量纲不同，为了处理方便，应先对原始数据进行归一化，记敏感变量的采样数据中共有M个样本，每个样本有N个敏感变量，则共有N个敏感变量向量，分别记为C_i(i＝1,2,…,N)，而c_ji(j＝1,2,…,M；i＝1,2,…,N)为第j样本的第i个敏感变量样本值。归一化计算公式为：

其中,E(C_i)指C_i的均值，Var(C_i)指C_i的标准差。

2)求敏感变量间的相关系数矩阵。经过归一化后的敏感变量向量为G_i(i＝1,2,…,N)，N个敏感变量的相关系数可以构成一个N×N的相关系数矩阵R，R中的每个元素记为R_ij(i＝1,2,…,N；j＝1,2,…,N)，每个元素的值为：

式中Conv(G_i,G_j)表示G_i和G_j的协方差，D(G_i)和D(G_j)分别表示G_i和G_j的方差。可以发现相关系数矩阵R是个对称矩阵。

3)求敏感变量正规化单位特征向量。对于N×N的相关系数矩阵R共可求得N个特征值，记为λ_i，根据由大到小依次排序为λ₁、λ₂、…、λ_N，再求出每个特征值所对应的正规化单位特征向量，记为L_i＝[l_1i l_2i…l_Ni]^T。

4)根据特征值的累计贡献率确定主成分，即敏感参数。累计贡献率是由特征值的大小所决定的，则前n成分的累计贡献率CR_n计算公式如下：

当累计贡献率CR_n≥ξ＝95％，其中ξ为控制值，这时的n为敏感参数个数，新的敏感参数正规化单位特征向量矩阵为步骤3)中前n个正规化单位特征向量L₁、L₂、…、L_n组成的矩阵L′，新的敏感参数的样本数据矩阵为Y＝D×L′，新的敏感参数即为Y的列属性。

其中，稳态权重因子SSWF为每个敏感参数的单个贡献率(或相关系数矩阵特征值)，即每个敏感参数稳态权重因子为：

步骤(6)、使用多项式最小二乘法拟合对每个敏感参数的采样区间数据进行滑动窗口H回归(示意图如图4所示)，得到敏感参数在各个采样点的回归值，用回归值代替原测量值可以去噪，而且多项式最小二乘法拟合含有敏感参数的变化信息，其在采样点的一阶导数即为该敏感参数在该采样点的变化快慢，并定义其为敏感参数的稳态指数SSI，根据敏感参数的稳态指数可以检测信号的稳态和非稳态。其中多项式最小二乘法拟合的具体步骤包括：对某个敏感参数在采样区间的序列x(j)进行多项式最小二乘法拟合时，首先定义一个长度为奇数的H长窗口，H＝2h+1，h为正整数。设在某一时刻，窗口内的信号样本为x(j-h),…,x(j),…,x(j+h)，其中x(j)为位于窗口中心的该敏感参数样本值。令窗口内的信号样本x(j-h),…,x(j),…,x(j+h)x′(1),…,x′(h+1),…,x′(2h+1)，其中x′(h+1)为位于窗口中心的该敏感参数样本值，对应的采样时刻t分别为1,2…,2h+1，则窗口内的拟合信号 则可以表示为时间t的函数，即：

其中，a＝[a₀ a₁,…,a_n]^T,n<2h+1为多项式最小二乘法拟合模型参数向量，r(t)＝[1,t,t²,…,tⁿ]^T为回归变量。应用最小二乘法就可以得到参数a的最优估计：

式中：

则经过多项式最小二乘法拟合后的拟合信号为

则敏感参数在各个采样点x(j)的回归值为:

其中敏感参数的稳态指数SSI为多项式最小二乘法拟合在采样点的一阶导数，即为该敏感参数在该采样点的变化快慢：

根据敏感参数的稳态指数就可以检测信号的稳态和非稳态。

步骤(7)、利用Dempster规则由各敏感参数的稳态权重因子SSWF和稳态指数SSI构建系统稳态指数SSSI，计算公式为：

设定阈值μ，根据检测精度来取值，一般取值为0.6～1，这里取μ＝0.7，从而判断加氢裂化流程系统是否处于稳态。

步骤(8)、为了消除系统大时滞性，根据系统稳态指数，获得产品质量离线化验时间前一个流程时滞时间窗口内系统基本处于稳态的稳态数据，并将流程时滞时间窗口内各敏感参数在采样点的数据的均值作为该敏感参数的特征值X，与该离线化验时间的产品质量Q组成训练集T的一个样本元素。

步骤(9)、使用随机森林回归算法(RFR)训练所建立的训练集T，建立一个稳态的加氢裂化流程产品质量在线预测模型。随机森林回归算法(RFR)的核心就是算法由多棵决策树组成，如图5所示，每棵树就是从根节点到叶节点根据特征变量不断分支的过程。具体步骤(简图如6所示)包括：

1)假定RF算法中需建立的决策树数量为100，对于每棵决策树，采用自助法(bootstrap)重采样方法有放回地从总训练集T中随机抽取和T样本容量相同的训练集T_i(i＝1,…,100)，并分别作为100棵决策树的训练集；

2)对于第i棵决策树的每个分支节点，采用不放回的采样方法从总特征变量M(本文中即为敏感参数特征集)中随机抽取m个特征变量作为特征子集M_ij(i＝1,…,100,j＝1,2,…)(j表示该决策树使用特征子集的个数)。通常情况下，每个分支节点的特征子集M_ij的特征变量数m为总特征变量M维度的开方，即 则

3)对每棵决策树，以T_i为训练样本，M_i为特征子集集合进行训练，从M_ij中选择一个最具有分类能力的变量对该节点进行分裂，每个决策树都得到最大限度的生产，而不进行剪枝。这样我们就可以得到一个随机森林回归模型{RF(T_i,M_i),i＝1,…,100}，其中，RF(T_i,M_i)为每棵决策树分类结果。

步骤(10)、将当前炼油工厂数据库中前一个流程时滞时间窗口内的敏感变量数据经过中值滤波、步骤(6)中PCA归一化和正规化特征向量矩阵变化处理后得到敏感参数数据，再通过多项式最小二乘法拟合、系统稳态检测，判断系统处于基本稳态后将敏感参数在流程时滞时间窗口内的数据均值作为该敏感参数的特征值，将敏感参数特征值向量X输入到训练好的随机森林产品质量在线预测模型，通过收集各个决策树的预测值，并对其加权均值作为产品质量预测结果，完成该时刻的产品质量Q检测，即：

最后，本申请的方法仅为较佳的实施方案，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。

一种加氢裂化流程产品质量在线预测方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。