专利摘要

基于相位斜率定位中心波峰的低相干干涉解调方法，利用低相干干涉测量外界大气压力，法布里-珀罗传感器将大气压力转化为腔长信息，当腔长引起的光程差和干涉仪扫描的光程差相匹配时形成干涉条纹。该方法首先对相位斜率和中心波峰峰值位置进行标定，通过多项式曲线拟合得到拟合系数；解调时，将相位斜率代入拟合表达式得到中心波峰峰值位置的估测值，与该估测值最近的波峰位置即为中心波峰峰值位置，从而实现解调。标定用的相位斜率的获取：对干涉信号进行离散傅立叶变换得到相位信息，然后对相位进行展开，最后对频率-展开后相位进行最小二乘线性拟合得到斜率；标定用的中心波峰峰值位置以压强-峰值位置的单调一致性为依据，通过递归比较得到。

说明书

技术领域

本发明涉及一种基于相位斜率定位中心波峰的低相干干涉解调方法，属于光纤传感领域。

背景技术

低相干干涉能够将外界被测物理量的变化反映在干涉条纹的平移信息上，不同于激光干涉得到的等幅干涉条纹，低相干干涉只在零光程差附近的局部位置产生明显的干涉条纹，对比度存在较大差异，更容易获取干涉条纹的平移信息，测量范围也不再局限于激光测量中的λ/4，因此，低相干干涉在光纤传感领域得到极大的应用，目前已广泛应用于温度、压力、折射率、位移等物理量的测量，此外在物体三维形貌检测和光学相干层析也有应用。

干涉条纹平移信息的获取主要有两种方法：一种方法是直接定位零光程位置，通过追踪零光程差位置的平移来获得整个干涉条纹的平移，利用干涉条纹的对比度或者包络峰值都可以实现零光程位置的定位，但是当信噪比较低时很难实现高精度定位；此外，还可以通过定位中心波峰的峰值位置来获取干涉条纹的平移信息，实验结果表明中心波峰的峰值位置比干涉条纹包络的峰值位置能更准确地反映整个干涉条纹的平移信息，但是中心波峰的准确定位问题目前还没有得到很好的解决，限制了该方法的应用；另一种方法是将干涉条纹的平移信息转化为相位信息，建立被测物理量和相位的一一对应关系，在频域实现低相干干涉的解调，相位斜率法、相移法和空间频域算法等都是基于相位提出的解调方法。

随着低相干干涉技术的发展，这两类解调方法都得到了逐步改进和完善，本发明专利通过综合上述两类方法提出了一种新的解调方法，该方法通过频域的相位斜率定位中心波峰，巧妙地结合了频域和时域信息，解决了中心波峰的准确定位问题。

发明内容

本发明的目的是解决中心波峰的准确定位问题，提供一种基于相位斜率定位中心波峰的低相干干涉解调方法。该方法利用相位斜率确定干涉条纹中心波峰的峰值位置，提高通过直接获取干涉条纹平移量进行解调的解调精度。

本发明提供的基于相位斜率定位中心波峰的低相干干涉解调方法，采用低精度的相位斜率解决中心波峰的高精度定位问题，通过中心波峰峰值位置的平移量来反映光程差的改变，进而实现高精度的解调，具体步骤是：

第1、进行标定实验：建立相位斜率和中心波峰峰值位置的一一映射关系；

第2、以相位斜率为自变量，中心波峰峰值位置为因变量，通过三次多项式拟合得到拟合表达式： 其中 为相位斜率，Y为中心波峰峰值位置；

第3、解调时，将相位斜率值代入拟合表达式得到中心波峰峰值位置的估测值，然后对干涉信号进行傅立叶滤波，在滤波后信号中寻找与估测值最接近的极大值点，该极大值点即为中心波峰峰值位置。

第1步所述的相位斜率和中心波峰峰值位置的对应关系的建立方法是：首先通过标定实验分别得到压强-相位斜率、压强-中心波峰峰值位置曲线，然后通过中间变量压强得到相位斜率-中心波峰峰值位置关系曲线。

第1步和第3步所述的相位斜率的获取方法是：首先对采集的离散干涉信号x(n)进行离散傅立叶变换转换到频域X(k)， 其中 为相位，A(k)为幅度，然后对相位 进行相位展开，最后对频率-展开后相位进行最小二乘线性拟合得到拟合直线，直线的斜率即为相位斜率。其中，相位展开的具体方法是：相位随着频率的增大呈单调减小，这是相位展开的理论依据，具体按照下面的递归表达式进行相位展开：

其中，u()是阶跃函数，m是幅度A(k)最大处对应的序列号。

上面所述的压强-中心波峰峰值位置对应关系的获取方法是：随着压强的单调增大，中心波峰的峰值位置会发生单调平移，这是压强-中心波峰峰值位置关系曲线获取的依据，具体步骤为：首先对起始压强下得到的干涉信号进行傅立叶滤波，以滤波后信号幅值最大处对应的CCD像素数为中心波峰峰值的基准位置；当压强以一定压强间隔增大到另一压强时，同样对干涉信号进行傅立叶滤波，在滤波后信号的所有极大值点中寻找第一个比起基准位置小的极大值点，该极大值点即为该压强下的中心波峰峰值位置，其中一定压强间隔的确定方法是保证压强变化引起的中心波峰峰值位置的平移量不大于干涉条纹的波长λ；依次类推，重新定义该压强下确定的中心波峰峰值位置为基准位置，当压强继续单调增大时，以上述同样的方法继续确定中心波峰峰值位置，如此循环往复，便获得了压强-中心波峰峰值位置的关系曲线。

相位斜率解调以及相位展开的理论依据：

一般常见的宽带光源的光谱都呈近似高斯分布，那么低相干干涉的光强可以表示为：

I(x)＝γexp{[-α(x-x₀)]²}cos[β(x-x₀)]                (1)

其中，α，β和γ是与光路系统有关的常数，x₀是零光程差位置对应在光楔中的坐标。

为了简化分析，我们定义：

f(x)＝γexp[-(αx)²]                                  (2)

那么式(2)的Fourier变换为F(jΩ)，F(jΩ)同样是高斯函数，Ω是频率。根据Fourier变换的时移和频移特性，式(1)的Fourier变换可以表示为：

G(jΩ)=1/2F[j(Ω+β)]e-jΩx0+1/2F(j[Ω-β])e-jΩx0---(3)]]>

在光频谱分析中，负频率成分没有实际的物理意义，不予考虑，因此，相频函数可以分别表示为：

从式(4)可以看出，相位斜率即与外界被测量直接相关，因此可以直接利用相位斜率进行低相干干涉解调，除此之外，从式(4)还可以得出，相位随着频率的增大而单调减小，这就是相位斜率解调和相位展开的理论依据。

本发明的有益效果及优点在于：

1、本方法利用低精度的相位斜率能够确定中心波峰峰值位置，实现了高精度的解调；

2、相对于直接提取平移信息进行解调的包络法，该发明方法不用提取干涉信号的包络，运算量有所减少，而且相对于包络法精度有很大提高；

3、不仅中心波峰可以用于解调，其他的波峰或波谷都可以用于解调，而且可以利用本发明方法进行任意波峰或波谷的定位；

附图说明

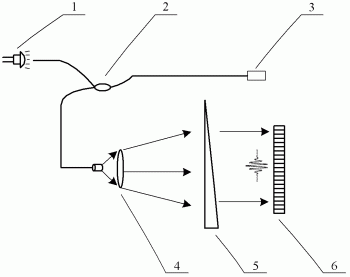
图1为空间扫描型低相干干涉光纤传感大气压力解调装置示意图；

图2分别为压强-相位斜率和压强-中心波峰峰值位置关系曲线，其中(a)为压强-相位斜率曲线；(b)为压强-中心波峰峰值位置曲线；

图3为随着压强单调递增变化的相位斜率-中心波峰峰值位置曲线；

图4为该发明方法的原理图，其中(a)为峰值间隔分析图；(b)为中心波峰峰值位置估测误差分析曲线；

图5为该发明方法的实验数据分析图，其中(a)为压强-中心波峰峰值位置曲线；(b)为解调误差曲线；

图6为该发明方法的稳定性分析图；

图7为解调误差对比图，其中(a)为相位斜率法误差；(b)为包络法误差。

具体实施方式

实施例

附图1是本发明方法涉及的一个针对外界大气压力测量的基于相位斜率定位中心波峰的低相干干涉解调装置图。

本发明的解调方法通过实验进行了验证，参见附图2-附图7。

宽带光源1发出的光经光耦合器2导入法布里-珀罗传感器3，3将大气压力信息转化为腔长信息，从3的两个端面反射的光发生近似双光束干涉，其中光程差为腔长的两倍，腔长随外界大气压强呈线性变化。被调制过的光信号从光耦合器2的出口导出，通过自聚焦准直透镜4并透过光楔5，最终到达线阵CCD 6，光楔5可以看作为空间分布的法布里-珀罗传感器，当5引起的光程差和3引起的光程差相匹配时，会在6相应的局部区域产生明显的低相干干涉条纹。

实验中需要的大气压强通过高精度、高稳定压力源产生，该压力源可以达到0.01kPa的控制精度，实验中控制压强以2kPa为间隔从60kPa单调递增到260kPa，压强改变时间间隔为5分钟。

第1步，进行标定实验，建立相位斜率和中心波峰峰值位置的一一对应关系。图2(a)为标定实验中得到的压强-相位斜率曲线，其中，相位斜率是通过下面的步骤得到的：首先对原始干涉信号x(n)进行傅立叶变换转换到频域X(k)， 其中 为相位，A(k)为幅度，根据幅度A(k)选择相位展开的范围为k∈[1552，1565]，然后以幅度A(k)最大处所对应的序列号m＝1558为基准相位，按照下面的递归表达式进行相位展开： 其中u()是阶跃函数，最后对展开后相位进行最小二乘线性拟合得到拟合直线，直线的斜率即为相位斜率。按照这种方法在每个压强下都可以得到一个相应的相位斜率，最终便获得图2(a)所示的随压强变化的相位斜率曲线；图2(b)为标定实验中得到的压强-中心波峰峰值位置曲线，其中，中心波峰峰值是通过下面步骤得到的：首先在压强为60kPa下对原始干涉信号进行傅立叶滤波，取滤波后信号幅值最大处对应的CCD像素数(2427)为中心波峰峰值的基准位置，然后压强增大到62kPa时，同样进行傅立叶滤波，在滤波信号的所有极大值点中寻找第一个基准位置(2427)小的极大值点，该极大值点(2407)即为62kPa下的中心波峰峰值位置；重新定义62kPa下确定的中心波峰峰值位置(2407)为基准位置，当压强继续以2kPa间隔单调增大时，以上述同样的方法继续确定中心波峰峰值位置，如此循环往复，便获得图2(b)所示的压强-中心波峰峰值位置曲线。从图2(a)可以看出，大气压强和相位斜率在整体上也呈现一定的线性关系，但局部区域线性度较差，可以应用于低精度解调场合；而从图2(b)可以看出，如果能够准确定位中心波峰的峰值位置，那么大气压强和中心波峰峰值位置无论在整体还是局部都能达到很高的线性度，能够实现高精度解调。

第2步，以第1步得到的相位斜率为自变量，中心波峰峰值位置为因变量，通过三次多项式拟合得到拟合表达式：Y＝-203.33-535.634X-9.87945X²-0.841612X³，其中，X为相位斜率，Y为中心波峰峰值位置。

第3步，进行实际的解调验证实验，解调时首先按照标定实验中相位斜率获取方法得到相位斜率，将其带入拟合表达式Y＝-203.33-535.634X-9.87945X²-0.841612X³，得到中心波峰峰值位置的估测值，然后对干涉信号进行傅立叶滤波，在滤波后信号中寻找与估测值最接近的极大值点，该极大值点即为中心波峰峰值位置。图4为该发明方法的原理分析图，其中图4(a)中的两条曲线分别为：曲线①为150kPa下得到的部分原始干涉信号，曲线②为150kPa下经过滤波后得到的相应部分的滤波信号。从图4(a)中的曲线②可以看出，相邻两个波峰之间的间距大约为52个像素间距，只要中心波峰峰值位置的估测值落在图中的阴影区域就能正确定位中心波峰的峰值位置。图4(b)为中心波峰峰值位置估测误差图，其中压强以2kPa为间隔从59kPa单调递增到259kPa，这与标定压强正好间隔开来，具有很好的代表性，从图4(b)可以看出通过拟合表达式计算出的中心波峰峰值位置的估测值和实际的中心波峰峰值位置相差在10个像素间隔内，估测值都在图4(a)的有效估测区间内，因此不会出现中心波峰的错误定位，因此本方法不仅是有效的，而且具有很好的稳定性和可靠性。

图5(a)为通过上面的3个步骤最终得到的压强-中心波峰峰值位置曲线图，可以看出在整个测量范围(59kPa-259kPa)内都没有出现波峰的错误定位(否则不会得到线性度这么好的关系曲线，如果出现了波峰的误判，在该压强下会出现曲线的跳跃，而且跳跃量大约为52)，因此，该发明方法是实际应用中完全可行的。图5(b)为利用确定后的中心波峰峰值位置进行解调后得到的误差图，可以看出，解调误差基本保持在±0.15kPa以内，满量程解调精度达到了0.75‰。

为了更全面地验证该方法的可行性，我们进行了稳定性实验分析，随机的选取了4个压强，压强分别为：83kPa、155kPa、177kPa和183kPa，在每个压强下连续采集200帧干涉信号，采集间隔为20ms，分别得到它们的中心波峰峰值位置估测误差曲线，详见图6。从图6可以看出，估测误差在恒定压强下存在一定的波动，波动大约为5个像素间隔，而且估测误差也都保持在10个像素间隔以内，相对于26个像素间隔波峰间距，完全能够保证中心波峰的准确定位，该发明方法具有很高的可靠性。

图7为采用不同解调方法得到的解调误差对比图，其中图7(a)和图7(b)分别为采用包络法和相位斜率法得到的解调误差，他们的最大解调误差都高达±1.25kPa，可见，相对于包络法和相位斜率法，该发明方法的解调精度得到了明显的提高。

基于相位斜率定位中心波峰的低相干干涉解调方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。