专利摘要

本发明提供了一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法，包括：(1).得到含多FACTS协调控制的电力系统单时滞模型的状态方程；(2).应用量子遗传算法生成个体；(3).设定约束条件，求解满足约束条件的个体的特征值和最小阻尼比；(4).判断迭代次数是否已到达限值，如果是则输出最小阻尼比对应的个体，否则进行步骤6；(5).判断个体的解是否满足约束条件，满足的，输出最小阻尼比对应的个体；否则返回步骤2；(6).根据得到的个体设计抗时滞协调控制器。通过本发明，可协调多台FACTS设备联合运行提高系统的动态稳定性；并且本发明对广域信号传输时滞具有较好的忍耐性，在较大的时滞范围内仍能发挥良好的协调作用。

权利要求

1.一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法，其特征在于，所述方法包括如下步骤：

(1).得到含多FACTS协调控制的电力系统单时滞模型的状态方程；

(2).应用量子遗传算法生成个体；

(3).设定约束条件，求解满足约束条件的个体的特征值和最小阻尼比；

(4).判断迭代次数是否已到达限值，如果是则输出最小阻尼比对应的个体，否则进行步骤6；

(5).判断个体的解是否满足约束条件，满足的，输出最小阻尼比对应的个体；否则返回步骤2；

(6).根据得到的个体设计抗时滞协调控制器。

2.根据权利要求1所述的方法，其特征在于，在所述步骤1中，含多FACTS协调控制的电力系统单时滞模型的状态方程：

$\stackrel{·}{x}\left(t\right)=\mathrm{Ax}\left(t\right)+A_{d}x(t-\tau )---\left(5\right)$

其中，A_d＝BKC；A、B、C是系数矩阵；K是待设计的多FACTS协调控制器系数矩阵。

3.根据权利要求1所述的方法，其特征在于，在所述步骤3中，设定的约束条件为：使线性矩阵不等式(10)和(11)成立；

$\left[\begin{array}{ccc}{\Phi }_{11}& {\Phi }_{12}& \tau A^{T}Z\\ *& {\Phi }_{22}& \tau A_{d}Z\\ *& *& -\mathrm{\tau Z}\end{array}\right]<0---\left(10\right)$

$\left[\begin{array}{ccc}{X}_{11}& X_{12}& N_2\\ *& X_{22}& N_1\\ *& *& Z\end{array}\right]\ge 0---\left(11\right)$

其中，${\Phi }_{11}=\mathrm{PA}+A^{T}P+N_1+N_1^T+\tau X_{11};$${\Phi }_{12}=P{A}_d-N_1+N_2^T+\tau X_{12};$${\Phi }_{22}=-N_2-N_2^T+\tau X_{22};\tau >0.$

4.根据权利要求1所述的方法，其特征在于，在所述步骤3中，求解满足约束条件的个体的特征值和最小阻尼比包括：

设定一个最小阻尼比的阈值，当各个体求得对应的系统阻尼比超出此阈值时停止求解；要求解系统的阻尼比必先求解其特征值λ；时滞系统(5)的特征方程是：

det(λI-A-A_de^-τλ)＝0   (12)

方程(12)是超越方程，采用PDE离散化方法来近似求解。

5.根据权利要求1所述的方法，其特征在于，在所述步骤4、5中，求得的最小阻尼比对应的个体就是所需的控制器系数矩阵K。

说明书

技术领域

本发明属于电力系统领域，具体涉及一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法。

背景技术

当前广域测量系统(WAMS)的PMU装置以GPS为采样基准，能全网同步采集机组和线路的电压、电流以及重要的开关保护信号；并能计算得到电压和电流相量、频率和频率变化率、机组和线路功率、发电机内电势(功角)以及根据机组键相信号实测机组功角；同时还能提供扰动触发的暂态记录。

随着广域测量系统(wide-area measurement system，WAMS)的逐步推广与完善，获取系统的部分状态变量和输出变量不再困难，而电力系统稳定本质上是一个全局问题，引入全局信息也有助于进一步提高全网稳定性。因此，结合WAMS技术进行协调控制研究也逐渐兴起，主要集中在系统阻尼控制和直流系统控制方面，与此相比采用WAMS技术的多FACTS协调控制研究较少。

发明内容

为克服上述缺陷，本发明提供了一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法，利用量子遗传算法寻优获得多FACTS协调控制器的最佳增益；而且在多台SVC的多机算例中进行时域仿真证明了所提算法的有效性。

为实现上述目的，本发明提供一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法，其改进之处在于，所述方法包括如下步骤：

(1).得到含多FACTS协调控制的电力系统单时滞模型的状态方程；

(2).应用量子遗传算法生成个体；

(3).设定约束条件，求解满足约束条件的个体的特征值和最小阻尼比；

(4).判断迭代次数是否已到达限值，如果是则输出最小阻尼比对应的个体，否则进行步骤6；

(5).判断个体的解是否满足约束条件，满足的，输出最小阻尼比对应的个体；否则返回步骤2；

(6).根据得到的个体设计抗时滞协调控制器。

本发明提供的优选技术方案中，在所述步骤1中，含多FACTS协调控制的电力系统单时滞模型的状态方程：

x·(t)=Ax(t)+Adx(t-τ)---(5)]]>

其中，A_d＝BKC；A、B、C是系数矩阵；K是待设计的多FACTS协调控制器系数矩阵。

本发明提供的第二优选技术方案中，在所述步骤3中，设定的约束条件为：使线性矩阵不等式(10)和(11)成立；

Φ11Φ12τATZ*Φ22τAdZ**-τZ<0---(10)]]>

X11X12N2*X22N1**Z≥0---(11)]]>

其中，Φ11=PA+ATP+N1+N1T+τX11;]]>Φ12=PAd-N1+N2T+τX12;]]>Φ22=-N2-N2T+τX22;τ>0;]]>

本发明提供的第三优选技术方案中，在所述步骤3中，求解满足约束条件的个体的特征值和最小阻尼比包括：

设定一个最小阻尼比的阈值，当各个体求得对应的系统阻尼比超出此阈值时停止求解；要求解系统的阻尼比必先求解其特征值λ；时滞系统(5)的特征方程是：

det(λI-A-A_de^-τλ)＝0   (12)

方程(12)是超越方程，采用PDE离散化方法来近似求解。

本发明提供的第四优选技术方案中，在所述步骤5、6中，求得的最小阻尼比对应的个体就是所需的控制器系数矩阵K。

与现有技术比，本发明提供的一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法，采用WAMS的输出反馈信号，针对信号的传输时滞，使用自由权矩阵时滞稳定定理作为判据，同时保证时滞系统的最小阻尼比在一定阈值之上，利用量子遗传算法寻优获得多FACTS协调控制器的最佳增益。最后在多台SVC的多机算例中进行时域仿真证明了所提算法的有效性。

附图说明

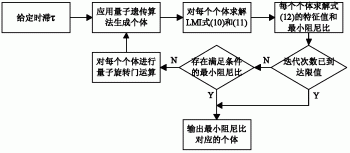
图1为基于自由权矩阵方法的多FACTS抗时滞协调控制方法的流程图。

图2为SVC数学模型的控制框图。

图3为基于WAMS的集中式协调控制流程图。

图4为含协调控制量的SVC动态模型。

具体实施方式

一种基于自由权矩阵方法的多FACTS抗时滞协调控制方法，其改进之处在于，所述方法包括如下步骤：

(1).得到含多FACTS协调控制的电力系统单时滞模型的状态方程；

(2).应用量子遗传算法生成个体；

(3).设定约束条件，求解满足约束条件的个体的特征值和最小阻尼比；

(4).判断迭代次数是否已到达限值，如果是则输出最小阻尼比对应的个体，否则进行步骤6；

(5).判断个体的解是否满足约束条件，满足的，输出最小阻尼比对应的个体；否则返回步骤2；

(6).根据得到的个体设计抗时滞协调控制器。

在所述步骤1中，含多FACTS协调控制的电力系统单时滞模型的状态方程：

x·(t)=Ax(t)+Adx(t-τ)---(5)]]>

其中，A_d＝BKC；A、B、C是系数矩阵；K是控制器系数矩阵。

在所述步骤3中，设定的约束条件为：使线性矩阵不等式(10)和(11)成立；

Φ11Φ12τATZ*Φ22τAdZ**-τZ<0---(10)]]>

X11X12N2*X22N1**Z≥0---(11)]]>

其中，Φ11=PA+ATP+N1+N1T+τX11;]]>Φ12=PAd-N1+N2T+τX12;]]>Φ22=-N2-N2T+τX22;τ>0;]]>

在所述步骤3中，求解满足约束条件的个体的特征值和最小阻尼比包括：

设定一个最小阻尼比的阈值，当各个体求得对应的系统阻尼比超出此阈值时停止求解；要求解系统的阻尼比必先求解其特征值λ；时滞系统(5)的特征方程是：

det(λI-A-A_de^-τλ)＝0   (12)

方程(12)是超越方程，采用PDE离散化方法来近似求解。

在所述步骤4、5中，求得的最小阻尼比对应的个体就是所需的控制器系数矩阵K。

通过以下实施例对基于自由权矩阵方法的多FACTS抗时滞协调控制方法做进一步描述。

在基于自由权矩阵方法的多FACTS抗时滞协调控制方法中：

1.确定系统模型和状态空间方程

1)本方法所涉及动态元件主要包括发电机和FACTS元件。其中发电机采用4阶实用模型，并安装一阶快速励磁。第i台发电机可以描述为：

δ·i=ω0(ωi-1)]]>

ω·i=12Hi[Pmi-Edi′Idi-Eqi′Iqi-Di(ωi-1)]]]>

Eqi′·=1Td0i′[Efdi′-(xdi-xdi′)Idi-Eqi′]---(1)]]>

Edi′·=1Tq0i′[-Edi′+(xqi-xqi′)Iqi]]]>

Efdi′·=1TA[-Efdi+KA(Vtrefi-Vt)]]]>

其中：δ表示发电机功角；ω表示发电机转子角速度；H_i表示发电机惯性时间常数的一半；P_m表示发电机机械功率；E′_d表示发电机交轴暂态电动势；E′_q表示发电机直轴暂态电动势；I_d表示发电机定子电流直轴分量；I_q表示发电机定子电流交轴分量；D表示发电机转子阻尼系数；T′_d0表示直轴开路暂态时间常数；T′_q0表示交轴开路暂态时间常数；x_d表示直轴同步电抗；x_q表示交轴同步电抗；x′_d表示直轴暂态电抗；x′_q表示交轴暂态电抗；E_fd表示励磁电动势；T_A表示励磁环节时间常数；K_A表示励磁环节放大倍数；V_tref表示励磁参考电压；V_t表示机端电压。

2)本方法拟采用多台SVC为例阐述所提协调控制算法。SVC数学模型的控制框图如图2所示。

SVC的动态表达式可以考虑为：

B·1=1T1[-B1+K(Vref-Vt)]B·SVC=1T0[B1-BSVC]---(2)]]>

其中，B_SVC为SVC的等效输出电纳值；B₁为中间变量；K为SVC控制器测量环节的增益；T₁和T₀表示时间常数；V_ref为参考电压；V_t为SVC控制节点的测量电压。

3)本发明以多FACTS协调控制机制集中式协调为例，提出如图3所示的协调控制示意图。协调控制器利用WAMS数据平台同步测量系统多点状态量和输出量，进行计算后得到各台FACTS设备的控制指令并下发，实现FACTS间的协调控制。

对于每台FACTS设备来说，接收到的协调控制变量u将作为控制器输入信号的一部分，与本地控制变量一起送入控制器。以图1的SVC模型为例，叠加了协调控制变量u的控制器模型如图4所示。

由此，全系统的状态空间模型可写成：

x·(t)=Ax(t)+Bu(t)y(t)=Cx(t)---(3)]]>

其中，x为系统状态变量；u为输入FACTS的协调控制变量；y为系统输出变量；A、B、C是系数矩阵。

4)本文设计的多FACTS协调控制器采用系统输出变量y作为输入。获取远端输出信号y经过WAMS传输需要一定时间；而且控制变量u由协调控制器发送至FACTS设备也存在时滞。假设最终总的时滞大小为τ，则多FACTS的静态输出反馈协调控制器可设计为

u(t)＝Ky(t-τ)  (4)

式中，K待设计的多FACTS协调为控制器的系数矩阵。

5)最终，由式(3)和式(4)可以得到含多FACTS协调控制的电力系统单时滞模型的状态方程：

x·(t)=Ax(t)+Adx(t-τ)---(5)]]>

其中，A_d＝BKC。

因此，设计抗时滞协调控制器的主要任务便是寻找合适的K，使得系统状态方程(5)保持稳定。

2、系统稳定性的判断依据：

本发明使用Lyapunov-Krasovskii稳定性定理，它的主要思想是通过构造一个合适的Lyapunov-Krasovskii泛函来获得使系统(5)稳定的充分条件。目前常采用的是含有二次型双积分项的泛函：

V(t,xt)=xT(t)Px(t)+∫t-d(t)txT(s)Qx(s)ds+]]>

∫-τ0∫t+θtx·T(s)Zx·(s)dsdθ---(6)]]>

其中，P＝P^T＞0，Q＝Q^T≥0和Z＝Z^T＞0是待定矩阵。对于任意合适维数的矩阵X=X11X12*X22≥0,]]>有

τη1T(t)Xη1(t)-∫t-d(t)tη1T(s)Xη1(s)ds≥0---(7)]]>

其中，η₁(t)＝[x^T(t) x^T(t-d(t))]^T。同时，根据牛顿-莱布尼茨公式，对于时滞项有

x(t-d(t))=x(t)-∫t-d(t)tx·(s)ds---(8)]]>

那么，根据自由权矩阵理论错误！未找到引用源。，对于任意合适维数的矩阵N1

2[x^T(t)N₁+x^T(t-d(t))N₂]×

和N2，有[x(t)-∫t-d(t)tx(s)ds-x(t-d(t))]=0]]>

此时，计算V(t，xt)沿系统(5)的导数，并结合式(8)和式(9)，可得如下定理：

定理1给定时滞τ＞0，如果存在满足上述要求的矩阵P，Z，X，N₁和N₂，使得如下两个线性矩阵不等式(10)和(11)成立，则时滞系统(5)是渐进稳定的。

Φ11Φ12τATZ*Φ22τAdZ**-τZ<0---(10)]]>

X11X12N2*X22N1**Z≥0---(11)]]>

其中

Φ11=PA+ATP+N1+N1T+τX11]]>

Φ12=PAd-N1+N2T+τX12]]>

Φ22=-N2-N2T+τX22]]>

定理1给出了判断时滞系统稳定的充分条件。在许多电力系统实际工程中，WAMS系统架设好后时滞τ通常是可以估计到的，此时再结合系统的状态方程，便可利用该定理作为系统稳定的判据。

3、利用寻优算法来获取合适的K

1)对系统的状态方程降节，本文采用Hankel降阶方法，它通过保证降阶前后系统的Hankel奇异值误差在较小范围内来实现降阶。

2)本文采用量子遗传算法寻求合适的控制器系数矩阵K。它的基本算法是：生成个体→测量→求解目标函数→与上一步最优值比较→生成量子旋转策略→转到第一步。

3)约束条件可设置为满足定理1中的式(10)和式(11)的解是否存在，如此来首先保证求出的系统是渐进稳定的。但可能会存在多组可行解，因此结合电力系统的实际需求，目标函数设定为使系统最小阻尼比最大化，即最小系统阻尼比越大，系统稳定水平越高，如此来保证系统能运行在强阻尼模式。同时为了确保控制的合理性，应设定一个最小阻尼比的阈值(如7％)，当超出此阈值时可停止寻优。

要求解系统的阻尼比必先求解其特征值λ。时滞系统(5)的特征方程是

det(λI-A-A_de^-τλ)＝0   (12)

这一方程是超越方程，不能直接求解。因此本文采用PDE离散化方法来近似求解。由于系统(5)的时滞微分方程在相互关联的边界条件下可转换为一组双曲型偏微分方程(Hyperbolic Partial Differential Equation，H-PDE)，因此通过对PDE进行精细离散化得到的增广矩阵，其特征值可近似于式(12)的解。

4)抗时滞的协调控制算法流程如图1所示。

需要声明的是，本发明内容及具体实施方式意在证明本发明所提供技术方案的实际应用，不应解释为对本发明保护范围的限定。本领域技术人员在本发明的精神和原理启发下，可作各种修改、等同替换、或改进。但这些变更或修改均在申请待批的保护范围内。

基于自由权矩阵方法的多FACTS抗时滞协调控制方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。