专利摘要

本发明公开了一种倾斜平面的纯相位全息投影方法，包括以下步骤：1)布设投影设备：将相位空间光调制器、分光棱镜、透镜和屏幕依次布设，在分光棱镜的同一侧布设单色激光器和偏振片，相位空间光调制器和计算机连接；2)确定系统中的参数，如倾斜平面的倾斜角，空间光调制器的采样间距和分辨率，透镜的焦距；3)利用坐标旋转，插值算法以及分数阶傅里叶变换和逆变换公式进行迭代计算，得到二维图像的相位；4)通过计算机将该相位全息图传输到相位空间光调制器中，再利用相位空间光调制器将相位全息图投影到指定位置的倾斜屏幕上。该全息投影方法可以使全息图重建的二维图像投影在透镜后任意距离的倾斜平面上，倾斜平面的距离可以很方便地控制。

权利要求

1.一种倾斜平面的纯相位全息投影方法，其特征在于：包括以下步骤：

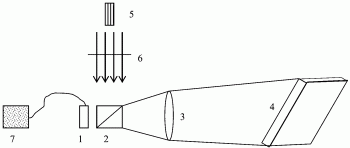
步骤1)，布设投影设备：将相位空间光调制器(1)、分光棱镜(2)、透镜(3)和倾斜屏幕(4)依次布设，使得相位空间光调制器(1)、分光棱镜(2)、透镜(3)和屏幕(4)处于同一条直线上；同时，在分光棱镜(2)的同一侧布设单色激光器(5)和偏振片(6)，偏振片(6)位于分光棱镜(2)和单色激光器(5)之间，单色激光器(5)发出的平面波通过偏振片(6)变为偏振光，偏振光通过分光棱镜(2)后可射入到相位空间光调制器(1)中；相位空间光调制器(1)和生成相位全息图的计算机(7)通过数据线连接；相位空间光调制器(1)所处的位置形成全息面x₀，屏幕(4)所处的位置形成倾斜平面x；

步骤2)，建立虚拟的参考平面x_r，参考平面x_r与倾斜平面x为同一中心并且与全息面x₀平行；

步骤3)，根据坐标旋转关系，建立参考平面x_r和倾斜平面x之间的光场分布关系：

F(u′，v′)＝FT[f(x′，y′)]

G(u，v)＝F(α^-1(u，v)，β^-1(u，v))＝F(u′，v′)    式(1)

g(x，y)＝FT^-1[G(u，v)]

式(1)中，f(x′，y′)为倾斜平面x的光场复振幅函数，x′，y′为f(x′，y′)的自变量，表示倾斜平面上各个点的坐标，F(u′，v′)为倾斜平面x的角谱函数，u′，v′为相应的角谱空间的坐标，G(u，v)为参考平面x_r的角谱函数，u，v为相应的角谱空间的坐标，(α^-1(u，v)，β^-1(u，v))表示从倾斜平面x到参考平面x_r的坐标变换，g(x，y)为参考平面x_r的光场复振幅函数，x，y为参考平面上各个点的坐标。FT为傅里叶变换，FT^-1为逆傅里叶变换；

步骤4)，测算透镜(3)的焦距f和参考面x_r的距离z之间的关系：

根据式(2)的分数阶傅里叶变换公式，建立全息面x₀和参考面x_r之间的光传播的函数：

$g\left(x\right)=\int F\left(x_0\right)·\exp \left[\mathrm{i\pi }(\frac{{x_0}^2}{\lambda f_e\tan (\mathrm{a\pi }/2)}+\frac{x^2}{\lambda f_e\tan (\mathrm{a\pi }/2)}-\frac{2x_{0}x}{\lambda f_e\sin (\mathrm{a\pi }/2)})\right]d{x}_0$    式(2)

式(2)中，g(x)为参考面x_r的光场复振幅函数，x为g(x)的自变量，F(x₀)为全息面x₀的光场复振幅函数，x₀为F(x₀)的自变量，i为虚数单位，λ为单色激光器(5)发出的平面波的波长，a为分数阶傅里叶变换的阶数，f_e为标准焦距，f_e＝f·sin(aπ/2)＝z/tan(aπ/4)，令Q＝sin(aπ/2)，R＝tan(aπ/4)，则f_e＝f·Q＝z/R；

其次，由f_e＝f·Q＝z/R可以得到参考平面x_r的距离z与透镜(3)的焦距f的关系如式(3)所示：

z＝f·R·Q    式(3)；

步骤5)，根据式(3)确定系统中分数阶傅里叶变换的阶数a后，利用式(1)和式(2)确定的全息面x₀和倾斜像平面x之间的光场传播关系进行迭代计算，得到倾斜平面x上二维图像在全息面x₀上的相位全息图；

步骤6)，根据步骤5)得到的相位全息图，通过计算机(7)将该相位全息图传输到相位空间光调制器(1)中，再利用相位空间光调制器(1)将相位全息图通过透镜(3)投影到指定位置的倾斜屏幕(4)上。

2.根据权利要求1所述的一种倾斜平面的纯相位全息投影方法，其特征在于：所述步骤5)包括以下步骤：

步骤5.1)，光场复振幅依照振幅因子乘以相位因子表示，令全息面x₀的振幅因子为1，相位因子为随机相位；

步骤5.2)，根据式(2)所示的参考平面x_r的光场复振幅函数，得到参考平面x_r上的光场复振幅分布；

步骤5.3)，根据式(1)表示的倾斜平面x光场复振幅与参考平面x_r光场复振幅的关系，得到倾斜平面x上的光场复振幅；

步骤5.4)，把倾斜平面x上的光场复振幅中的振幅因子用将要重建的二维图像的灰度值代替，倾斜平面x上的光场复振幅中的相位因子保持不变；

步骤5.5)，再利用式(1)所示的倾斜平面x光场复振幅与参考平面x_r光场复振幅的关系，得到参考平面x_r上的光场复振幅；

步骤5.6)，再利用如式(4)所示的分数阶傅里叶变换公式逆变换公式测算出全息面x₀上的光场复振幅；

$F\left(x_0\right)=\int g\left(x\right)·\exp \left[\mathrm{i\pi }(\frac{{x_0}^2}{\lambda f_e\tan (-\mathrm{a\pi }/2)}+\frac{x^2}{\lambda f_e\tan (-\mathrm{a\pi }/2)}-\frac{2x_{0}x}{\lambda f_e\sin (-\mathrm{a\pi }/2)})\right]dx$式(4)；

步骤5.7)，将全息面x₀上的光场复振幅中的振幅因子用单位强度值1来代替，全息面x₀上的光场复振幅中的相位因子保持不变；

步骤5.8)，重复步骤5.1)至5.7)，进行反复迭代，直到全息面x₀上的相邻两次光场复振幅中的相位因子的均方根误差小于0.05后停止迭代，得到全息面x₀上的光场复振幅的相位因子，依照式(5)将停止迭代后得到的全息面x₀上的光场复振幅的相位因子进行相位编码，得到相位全息图；

$\phi =255-\left[\frac{({\phi }_0+\pi )\times 255}{2\pi }\right]$      式(5)

式(5)中，φ₀表示迭代后得到的全息面x₀上的光场复振幅的相位因子值，φ表示经过相位编码后得到的全息面x₀上的光场复振幅的相位因子值。

说明书

技术领域

本发明涉及一种全息投影方法，特别是涉及一种倾斜平面的纯相位全息投影方法。

背景技术

对于传统的计算倾斜平面的光场分布在空间中的传播来说，一般采用的方法是：首先通过角谱域的坐标旋转来计算参考平面的光场分布，然后再通过光在空间中平行平面的传播理论(如角谱法)来计算全息面上的光场分布，这种情况下，在全息面上得到的光场分布是复振幅的形式，即同时包含振幅信息与相位信息，因此要实现纯相位调制，必须对复振幅进行相位编码，从而增加了复杂性与误差。而另一方面，对于传统的纯相位全息投影来说，相位全息图的生成是采用经典的Gerschberg-Saxton(GS)迭代算法，这是一种基于傅里叶变换的迭代算法，它可以通过迭代直接得到二维图像的相位信息而不需编码等计算。但是在这种技术中，成像面与全息面是平行的，相位全息图只能在空间中与全息面平行的平面上进行投影，并且投影成像始终成在透镜的后焦面上，成像距离也就是透镜的焦距，对于实际应用有一定的限制。

发明内容

发明目的：提供一种倾斜平面的纯相位全息投影方法，可以使全息图重建的二维图像投影在空间中的任意距离的倾斜平面上，而不需要改变透镜的焦距来控制成像的距离；并且调制方式为纯相位调制，降低传统方法的复杂性与误差度。

技术方案：为解决上述技术问题，本发明的一种倾斜平面的纯相位全息投影方法，包括以下步骤：

步骤1)，布设投影设备：将相位空间光调制器1、分光棱镜2、透镜3和倾斜屏幕4依次布设，使得相位空间光调制器1、分光棱镜2、透镜3和屏幕4处于同一条直线上；同时，在分光棱镜2的同一侧布设单色激光器5和偏振片6，偏振片6位于分光棱镜2和单色激光器5之间，单色激光器5发出的平面波通过偏振片6变为偏振光，偏振光通过分光棱镜2后可射入到相位空间光调制器1中；相位空间光调制器1和生成相位全息图的计算机7通过数据线连接；相位空间光调制器1所处的位置形成全息面x₀，屏幕4所处的位置形成倾斜平面x；

步骤2)，建立虚拟的参考平面x_r，参考平面x_r与倾斜平面x为同一中心并且与全息面x₀平行；

步骤3)，根据坐标旋转关系，建立参考平面x_r和倾斜平面x之间的光场分布关系：

F(u′，v′)＝FT[f(x′，y′)]

G(u，v)＝F(α^-1(u，v)，β^-1(u，v))＝F(u′，v′)    式(1)

g(x，y)＝FT^-1[G(u，v)]

式(1)中，f(x′，y′)为倾斜平面x的光场复振幅函数，x′，y′为f(x′，y′)的自变量，表示倾斜平面上各个点的坐标，F(u′，v′)为倾斜平面x的角谱函数，u′，v′为相应的角谱空间的坐标，G(u，v)为参考平面x_r的角谱函数，u，v为相应的角谱空间的坐标，(α^-1(u，v)，β^-1(u，v))表示从倾斜平面x到参考平面x_r的坐标变换，g(x，y)为参考平面x_r的光场复振幅函数，x，y为参考平面上各个点的坐标。FT为傅里叶变换，FT^-1为逆傅里叶变换；

步骤4)，测算透镜3的焦距f和参考面x_r的距离z之间的关系：

根据式(2)的分数阶傅里叶变换公式，建立全息面x₀和参考面x_r之间的光传播的函数：

g(x)=∫F(x0)·exp[iπ(x02λfetan(aπ/2)+x2λfetan(aπ/2)-2x0xλfesin(aπ/2))]dx0]]>    式(2)

式(2)中，g(x)为参考面x_r的光场复振幅函数，x为g(x)的自变量，F(x₀)为全息面x₀的光场复振幅函数，x₀为F(x₀)的自变量，i为虚数单位，λ为单色激光器5发出的平面波的波长，a为分数阶傅里叶变换的阶数，f_e为标准焦距，f_e＝f·sin(aπ/2)＝z/tan(aπ/4)，令Q＝sin(aπ/2)，R＝tan(aπ/4)，则f_e＝f·Q＝z/R；

其次，由f_e＝f·Q＝z/R可以得到参考平面x_r的距离z与透镜(3)的焦距f的关系如式(3)所示：

z＝f·R·Q        式(3)；

步骤5)，根据式(3)确定系统中分数阶傅里叶变换的阶数a后，利用式(1)和式(2)确定的全息面x₀和倾斜像平面x之间的光场传播关系进行迭代计算，得到倾斜平面x上二维图像在全息面x₀上的相位全息图；

步骤6)，根据步骤5)得到的相位全息图，通过计算机7将该相位全息图传输到相位空间光调制器1中，再利用相位空间光调制器1将相位全息图通过透镜3投影到指定位置的倾斜屏幕4上。

其中，所述步骤5)包括以下步骤：

步骤5.1)，光场复振幅依照振幅因子乘以相位因子表示，令全息面x₀的振幅因子为1，相位因子为随机相位；

步骤5.2)，根据式(2)所示的参考平面x_r的光场复振幅函数，得到参考平面x_r上的光场复振幅分布；

步骤5.3)，根据式(1)表示的倾斜平面x光场复振幅与参考平面x_r光场复振幅的关系，得到倾斜平面x上的光场复振幅；

步骤5.4)，把倾斜平面x上的光场复振幅中的振幅因子用将要重建的二维图像的灰度值代替，倾斜平面x上的光场复振幅中的相位因子保持不变；

步骤5.5)，再利用式(1)所示的倾斜平面x光场复振幅与参考平面x_r光场复振幅的关系，得到参考平面x_r上的光场复振幅；

步骤5.6)，再利用如式(4)所示的分数阶傅里叶变换公式逆变换公式测算出全息面x₀上的光场复振幅；

F(x0)=∫g(x)·exp[iπ(x02λfetan(-aπ/2)+x2λfetan(-aπ/2)-2x0xλfesin(-aπ/2))]dx]]>式(4)；

步骤5.7)，将全息面x₀上的光场复振幅中的振幅因子用单位强度值1来代替，全息面x₀上的光场复振幅中的相位因子保持不变；

步骤5.8)，重复步骤5.1)至5.7)，进行反复迭代，直到全息面x₀上的相邻两次光场复振幅中的相位因子的均方根误差小于0.05后停止迭代，得到全息面x₀上的光场复振幅的相位因子，依照式(5)将停止迭代后得到的全息面x₀上的光场复振幅的相位因子进行相位编码，得到相位全息图；

φ=255-[(φ0+π)×2552π]]]>        式(5)

式(5)中，φ₀表示迭代后得到的全息面x₀上的光场复振幅的相位因子值，φ表示经过相位编码后得到的全息面x₀上的光场复振幅的相位因子值。

有益效果：1.倾斜平面的纯相位调制。本发明将传统的倾斜平面在空间中的传播理论与Gerschberg-Saxton(GS)算法相结合，得到了倾斜平面图像的相位恢复算法，这种算法以倾斜平面到全息面的传播以及全息面到倾斜平面的逆传播为基础，分别在倾斜平面和全息面施加振幅约束来进行循环迭代，最终在全息面上得到优化的相位分布。利用纯相位空间光调制器，可以在空间中的倾斜平面得到二维图像的重建像。与传统的倾斜平面成像调制相比，这种方法得到的全息图是纯相位全息图，具有非常高的光衍射效率，并且通过一定次数的迭代计算之后，重建图像的误差可以很小，成像质量比传统方法更加高。

2.成像距离可以随意改变。本发明采用的全息投影方法可以把相位全息图投影在透镜后的任意距离的倾斜平面上，不需要根据成像的距离来改变透镜焦距。纯相位全息图是采用基于分数阶傅里叶变换的迭代算法生成，使用相位型空间光调制器进行投影时，根据分数阶傅里叶变换的特点，利用这种方法生成的全息图可以把图像投影在透镜后的任意距离的倾斜平面上。因此，本发明不仅实现了在倾斜平面上的纯相位投影，并且可以很容易的控制倾斜成像面距离。

附图说明

图1是本发明的步骤1)的投影设备位置图；

图2是本发明的步骤1)中各个平面之间的关系图；

图3是本发明的相位全息图的迭代算法图示。

具体实施方式

下面结合附图对本发明做更进一步的解释。

如图1所示，一种倾斜平面的纯相位全息投影方法，包括以下步骤：

步骤1)，布设投影设备：将相位空间光调制器1、分光棱镜2、透镜3和倾斜屏幕4依次布设，使得相位空间光调制器1、分光棱镜2、透镜3和屏幕4处于同一条直线上。同时，在分光棱镜2的同一侧布设单色激光器5和偏振片6，偏振片6位于分光棱镜2和单色激光器5之间，单色激光器5发出的平面波通过偏振片6变为偏振光，偏振光通过分光棱镜2后可射入到相位空间光调制器1中。相位空间光调制器1和生成相位全息图的计算机7通过数据线连接。相位空间光调制器1所处的位置形成全息面x₀，屏幕4所处的位置形成倾斜平面x。

步骤2)，建立虚拟的参考平面x_r，参考平面x_r与倾斜平面x为同一中心并且与全息面x₀平行。

步骤3)，根据坐标旋转关系，建立参考平面x_r和倾斜平面x之间的光场分布关系：

F(u′，v′)＝FT[f(x′，y′)]

G(u，v)＝F(α^-1(u，v)，β^-1(u，v))＝F(u′，v′)    式(1)

g(x，y)＝FT^-1[G(u，v)]

式(1)中，f(x′，y′)为倾斜平面x的光场复振幅函数，x′，y′为f(x′，y′)的自变量，表示倾斜平面上各个点的坐标，F(u′，v′)为倾斜平面x的角谱函数，u′，v′为相应的角谱空间的坐标，G(u，v)为参考平面x_r的角谱函数，u，v为相应的角谱空间的坐标，(α^-1(u，v)，β^-1(u，v))表示从倾斜平面x到参考平面x_r的坐标变换，g(x，y)为参考平面x_r的光场复振幅函数，x，y为参考平面上各个点的坐标。FT为傅里叶变换，FT^-1为逆傅里叶变换。

步骤4)，测算透镜3的焦距f和参考面x_r的距离z之间的关系：

根据式(2)的分数阶傅里叶变换公式，建立全息面x₀和参考面x_r之间的光传播的函数：

g(x)=∫F(x0)·exp[iπ(x02λfetan(aπ/2)+x2λfetan(aπ/2)-2x0xλfesin(aπ/2))]dx0]]>    式(2)

式(2)中，g(x)为参考面x_r的光场复振幅函数，x为g(x)的自变量，F(x₀)为全息面x₀的光场复振幅函数，x₀为F(x₀)的自变量，i为虚数单位，λ为单色激光器5发出的平面波的波长，a为分数阶傅里叶变换的阶数，f_e为标准焦距，f_e＝f·sin(aπ/2)＝z/tan(aπ/4)，令Q＝sin(aπ/2)，R＝tan(aπ/4)，则f_e＝f·Q＝z/R。

其次，由f_e＝f·Q＝z/R可以得到参考平面x_r的距离z与透镜3的焦距f的关系如式(3)所示：

z＝f·R·Q         式(3)；

步骤5)，根据式(3)确定系统中分数阶傅里叶变换的阶数a后，利用式(1)和式(2)确定的全息面x₀和倾斜像平面x之间的光场传播关系进行迭代计算，得到倾斜平面x上二维图像在全息面x₀上的相位全息图。

其中，步骤5)包括以下步骤：

步骤5.1)，光场复振幅依照振幅因子乘以相位因子表示，令全息面x₀的振幅因子为1，相位因子为随机相位。

步骤5.2)，根据式(2)所示的参考平面x_r的光场复振幅函数，得到参考平面x_r上的光场复振幅分布。

步骤5.3)，根据式(1)表示的倾斜平面x光场复振幅与参考平面x_r光场复振幅的关系，得到倾斜平面x上的光场复振幅。

步骤5.4)，把倾斜平面x上的光场复振幅中的振幅因子用将要重建的二维图像的灰度值代替，倾斜平面x上的光场复振幅中的相位因子保持不变。

二维图像的灰度值在计算机matlab软件中用imread语句处理图片，即可得到图像的灰度值。在程序中用语句A＝imread(‘B.jpg’)，B是图片名，格式为jpg，这个语句意思表示的就是输出图片B的灰度，得到的A就是图像的灰度，在图片中称作灰度。本发明中，在matlab软件中使用上述语句获取二维图像的灰度值。将要重建的二维图像是指将要投影在屏幕上的二维图像。

步骤5.5)，再利用式(1)所示的倾斜平面x光场复振幅与参考平面x_r光场复振幅的关系，得到参考平面x_r上的光场复振幅。

步骤5.6)，再利用如式(4)所示的分数阶傅里叶变换公式逆变换公式测算出全息面x₀上的光场复振幅；

F(x0)=∫g(x)·exp[iπ(x02λfetan(-aπ/2)+x2λfetan(-aπ/2)-2x0xλfesin(-aπ/2))]dx]]>式(4)；

其中，(4)式各字母含义与(2)式中字母含义一致。

步骤5.7)，将全息面x₀上的光场复振幅中的振幅因子用单位强度值1来代替，全息面x₀上的光场复振幅中的相位因子保持不变。

步骤5.8)，重复步骤5.1)至5.7)，进行反复迭代，直到全息面x₀上的相邻两次光场复振幅中的相位因子的均方根误差小于0.05后停止迭代，得到全息面x₀上的光场复振幅的相位因子，依照式(5)将停止迭代后得到的全息面x₀上的光场复振幅的相位因子进行相位编码，得到相位全息图；

φ=255-[(φ0+π)×2552π]]]>         式(5)

式(5)中，φ₀表示迭代后得到的全息面x₀上的光场复振幅的相位因子值，φ表示经过相位编码后得到的全息面x₀上的光场复振幅的相位因子值。

步骤6)，根据步骤5)得到的相位全息图，通过计算机7将该相位全息图传输到相位空间光调制器1中，再利用相位空间光调制器1将相位全息图通过透镜3投影到指定位置的倾斜屏幕4上。

本发明中，相位全息图通过计算机7加载到相位空间光调制器1中，单色激光器5发出的单色绿光通过偏振片6变为偏振光，然后通过分光棱镜2后，射入空间光调制器1，光波在相位空间光调制器1中进行相位调制后反射出，通过分光棱镜2和透镜3之后，在透镜3后的空间进行成像，倾斜平面与透镜的距离可以通过控制分数阶傅里叶变换的阶数来调节，不同的阶数对应不同的距离，图像可以被投影到任意距离的倾斜平面上而不受透镜焦距的限制。

本发明的倾斜平面的全息投影方法利用角谱空间的坐标旋转以及分数阶傅里叶变换公式来测算相位全息图，并且在全息投影再现二维图像的过程中，采用分数阶傅里叶变换对应的光路结构来实现这一过程。在全息图的测算过程中，把倾斜平面之间光场的传播理论与用传统GS迭代算法相结合，并且用分数阶傅里叶变换来计算光在空间中的衍射传播，并最终通过迭代得到倾斜平面的纯相位全息图。在重建过程中，相位全息图被加载到相位空间光调制器1中，通过重建光波的照射对每个像素点的光产生相位调制，并在透镜3后的倾斜平面上成像。

实施例：采用单色激光器5发出的波长为532纳米的单色绿光来进行投影；相位空间光调制器1采用美国BNS公司生产的相位空间光调制器，其规格为512×512像素，像素间距为15微米；透镜3的焦距f为0.5米。

透镜3后设置倾斜平面4，倾斜平面的倾斜角度为α＝30°，方向为绕y轴旋转。在与光轴垂直的平面上建立虚拟的参考平面，参考平面与倾斜平面有相同的中心，并且与全息面平行。全息面、透镜3与参考平面组成一个分数阶傅里叶变换的光学系统，参考平面到透镜的距离为z＝0.7m，因此根据阶数和距离的公式z＝f·tan(aπ/4)·sin(aπ/2)，很容易计算出系统的分数阶傅里叶变换的阶数为a＝1.25，然后以参考平面的中心所在的y轴为旋转轴，旋转30°即可得到倾斜平面的位置。其中，根据分数阶傅里叶变换的理论模型，相位空间光调制器1到透镜3的距离与透镜3到参考平面x_r的距离z是一样的。

根据上述确定的参数，采用图3所示的迭代算法在倾斜平面与全息面之间进行迭代传播，在全息面上施加单位振幅约束条件，在倾斜平面施加二维图像的灰度作为约束条件，经过迭代之后，在全息面上得到相位分布，经过编码后得到相位全息图。

得到的相位全息图经过计算机7加载到空间光调制器1中，就能够在倾斜平面4得到相应的重建的二维图像。因此，如果想要在透镜之后任意距离的倾斜平面上投影成像，只要确定倾斜平面的角度以及平面的中心与透镜的距离，然后用倾斜平面的传播计算方法以及迭代算法得到相位全息图，即可在想要成像的倾斜平面上投影重建图像，并且这种投影方式为纯相位投影，具有非常高的光衍射效率和成像质量。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。

一种倾斜平面的纯相位全息投影方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。