专利摘要

本发明公开了一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，具体包括：一、确定导弹气动参数和建立大气模型的参数；二、根据导弹气动参数和大气模型的参数建立导弹运动方程组；三、对导弹运动方程组进行线性化处理；四、将线性化处理方程组中加入法向加速度导数方程，得到解析求解方程组；五、确定下滑段弹道要满足的末端约束和路径约束；六、根据解析求解方程组和最优控制指标函数确定最优控制量u；七、求解最优控制量u得到解析制导律，使导弹下滑段弹道满足末端约束和路径约束。优点在于：保证了导弹在达到规定末端高度的同时，满足弹道倾角、速度、法向加速度以及法向加速度一阶导数的约束，改善了导弹的飞行品质。

权利要求

1.一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，其特征在于，包括以下步骤：

步骤一、根据空射巡航导弹外形确定导弹气动参数，同时建立大气模型的参数；

导弹气动参数包括：导弹的升力系数C_L和导弹的阻力系数C_D；

$\left\{\begin{array}{c}{C}_L=0.07907\alpha +0.08512\\ C_D=7.852\times {10}^{-4}{\alpha }^2+9.029\times {10}^{-4}\alpha +0.2818M^2-0.2636M+0.08394\end{array}\right.$

α为导弹攻角，M为马赫数，计算式为 其中V为导弹相对大气的速度，V_s为当地声速；

大气模型的参数包括空气密度ρ和当地声速V_s：

$\left\{\begin{array}{c}\rho =1.2353\times e^{-1.06\times {10}^{-4}h}\\ V_s=340.63-4.076\times {10}^{-3}h\end{array}\right.$

h为导弹所处的飞行高度；

步骤二、根据导弹气动参数和大气模型的参数建立导弹运动方程组；

导弹运动方程组如下：

$\left\{\begin{array}{c}\frac{dV}{dt}=-gsin\theta -\frac{D}{m}\\ \frac{d\theta }{dt}=-\frac{g\cos \theta }{V}+\frac{L}{mV}\\ \frac{dx}{dt}=V\cos \theta \\ \frac{dh}{dt}=V\sin \theta \end{array}\right.$

其中，t为导弹的飞行时间，θ为弹道倾角，x为导弹的水平飞行距离，m为导弹质量，g为重力加速度；L和D分别为导弹的升力和导弹的阻力，计算式如下：

$\left\{\begin{array}{c}L=L(V,\alpha ,h)=\frac{1}{2}{\mathrm{\rho V}}^2{C}_{L}S\\ D=D(V,\alpha ,h)=\frac{1}{2}{\mathrm{\rho V}}^2{C}_{D}S\end{array}\right.$

S是导弹的参考面积；

步骤三、对导弹运动方程组进行线性化处理，得到线性化处理方程组；

步骤四、将线性化处理方程组中加入法向加速度导数方程，得到解析求解方程组；

法向加速度一阶导数方程为： 法向加速度二阶导数方程为：$\frac{d{\stackrel{·}{a}}_n}{{\mathrm{dt}}_{go}}=-{\stackrel{··}{a}}_n;$

其中 为法向加速度的一阶导数， 为法向加速度的二阶导数；

解析求解方程组如下：

$\left\{\begin{array}{c}\frac{dV}{{\mathrm{dt}}_{go}}=\frac{a_n+g}{K}+g\theta \\ \frac{d\theta }{{\mathrm{dt}}_{go}}=-\frac{a_n}{V_0}\\ \frac{dx}{{\mathrm{dt}}_{go}}=-V_0\\ \frac{dh}{{\mathrm{dt}}_{go}}=-V_0\theta \\ \frac{{\mathrm{da}}_n}{{\mathrm{dt}}_{go}}=-{\stackrel{·}{a}}_n\\ \frac{d{\stackrel{·}{a}}_n}{{\mathrm{dt}}_{go}}=-{\stackrel{··}{a}}_n=-u\end{array}\right.$

表示把 当作控制量；

步骤五、导弹下滑时确定下滑段弹道要满足的末端约束和路径约束；

末端约束具体设置如下：

$\left\{\begin{array}{cc}h\left(t_0\right)=h_0& h\left(t_f\right)=h_f\\ \theta \left(t_0\right)=0& \theta \left(t_f\right)=0\\ x\left(t_0\right)=0& x\left(t_f\right)=free\\ V\left(t_0\right)=V_0& V\left(t_f\right)=V_f\\ a_n\left(t_0\right)=a_{n0}& a_n\left(t_f\right)=a_{nf}\\ {\stackrel{·}{a}}_n\left(t_0\right)={\stackrel{·}{a}}_{n0}& {\stackrel{·}{a}}_n\left(t_f\right)={\stackrel{·}{a}}_{nf}\end{array}\right.$

其中，h(t₀)＝h₀表示t＝t₀时刻的高度为h₀，h(t_f)＝h_f表示在t＝t_f时刻的高度为h_f，θ(t₀)＝0表示t＝t₀时刻的弹道倾角为0；θ(t_f)＝0表示t＝t_f时刻的弹道倾角为0，x(t₀)＝0表示t＝t₀时刻导弹的水平飞行距离为0，x(t_f)＝free表示t＝t_f时刻导弹的水平飞行距离无约束，V(t₀)＝V₀表示t＝t₀时刻导弹相对大气的速度为常数V₀，V(t_f)＝V_f表示t＝t_f时刻导弹相对大气的速度为V_f，a_n(t₀)＝a_n0表示t＝t₀时刻导弹法向加速度为a_n0，a_n(t_f)＝a_nf表示t＝t_f时刻导弹法向加速度为a_nf， 表示t＝t₀时刻法向加速度的一阶导数为 表示t＝t_f时刻法向加速度的一阶导数为

路径约束包括导弹的速度和法向加速度约束，如下：

$\left\{\begin{array}{c}{V}_{\min }\le V\le V_{\max }\\ a_{nmin}\le a_n\le a_{nmax}\end{array}\right.$

其中V_min，V_max，a_nmin和a_nmax根据具体导弹的设计参数决定；

步骤六、选取最优控制的指标函数，根据解析求解方程组和指标函数确定最优控制量u；

选取能量控制为指标函数J：

$J={\int }_0^{t_f}\frac{1}{2}{u}^2{\mathrm{dt}}_{go}$

步骤七、求解最优控制量u得到解析制导律，使导弹下滑段弹道满足末端约束和路径约束；

基于最优控制理论中的极小值原理，对最优控制问题进行解析求解，得到解析制导律为：

u＝16x₁-120x₂+480x₃-840x₄

其中，$x_1=-\frac{{\stackrel{·}{a}}_n-{\stackrel{·}{a}}_{nf}}{{\tau }_{go}};x_2=\frac{a_n+{\stackrel{·}{a}}_{nf}{\tau }_{go}-a_{nf}}{{{\tau }_{go}}^2},x_3=\frac{-V\theta +\frac{{\stackrel{·}{a}}_{nf}{{\tau }_{go}}^2}{2}-a_{nf}{\tau }_{go}}{{{\tau }_{go}}^3},$$x_4=\frac{h-h_f+\frac{{\stackrel{·}{a}}_{nf}{{\tau }_{go}}^3}{6}-\frac{a_{nf}{{\tau }_{go}}^2}{2}}{{{\tau }_{go}}^4}$

${\tau }_{go}=\frac{K}{g}(V-V_f)+\frac{V}{g}\theta +\frac{K}{V}(h-h_f)$

τ_go是剩余飞行时间。

2.如权利要求1所述的一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，其特征在于，所述步骤三具体为：

导弹运动方程组的线性化处理包含：

(1)引入法向加速度a_n：

(2)设升阻比K为常数：

(3)将速度简化处理：将导弹运动方程组中导弹的实时速度V设为常数V₀；

(4)引入剩余时间：导弹的飞行时间t替换为剩余飞行时间t_go，t_go与t的关系如下：t_go＝t_f-t；

t_f为导弹的总飞行时间；

得到线性化处理方程组：

$\left\{\begin{array}{c}\frac{dV}{{\mathrm{dt}}_{go}}=\frac{a_n+g}{K}+g\theta \\ \frac{d\theta }{{\mathrm{dt}}_{go}}=-\frac{a_n}{V_0}\\ \frac{dx}{{\mathrm{dt}}_{go}}=-V_0\\ \frac{dh}{{\mathrm{dt}}_{go}}=-V_0\theta \end{array}\right.$

3.如权利要求1所述的一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，其特征在于，所述步骤五中末端约束是指：导弹在下滑段末端点要满足的约束；包括末端高度约束、速度约束、弹道倾角约束、法向加速度约束和末端法向加速度一阶导数约束。

4.如权利要求1所述的一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，其特征在于，所述步骤五中：导弹的速度V_max＝300m/s，V_min＝150m/s；法向加速度a_nmin＝-10g，a_nmax＝10g。

说明书

技术领域

本发明属于航空航天技术、武器领域，涉及空射巡航导弹下滑段多约束制导律的解析解，具体是指一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法。

背景技术

空射巡航导弹是指从空中发射的巡航导弹，它的弹道包括下滑段、平飞段和俯冲段。下滑段不仅需要满足多项末端状态约束(主要包括末端高度、弹道倾角、速度和攻法向加速度约束)，还要尽可能缩短下滑段时间，以提高隐蔽性。

传统的制导方法是弹道跟踪制导，所用标准弹道可以通过方案弹道规划和弹道优化等方法得到；跟踪标准弹道的制导律的设计通常使用PID控制、反馈线性化等方法。跟踪制导的优点是制导律设计相对简单，缺点在于过于依赖标准弹道，以及在大扰动下的精度相对较差。

发明内容

本发明针对现有技术中，导弹下滑段不能快速下降，以及导弹下滑段末端不能平稳拉起等问题；提出了一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，保证了导弹在达到规定末端高度的同时，满足弹道倾角、速度、法向加速度以及法向加速度一阶导数的约束，改善了导弹的飞行品质。

具体步骤如下：

步骤一、根据空射巡航导弹外形确定导弹气动参数，同时建立大气模型的参数；

导弹气动参数包括：导弹的升力系数C_L和导弹的阻力系数C_D

CL=0.07907α+0.08512CD=7.852×10-4α2+9.029×10-4α+0.2818M2-0.2636M+0.08394]]>

α为导弹攻角，M为马赫数，计算式为 其中V为导弹相对大气的速度，V_s为当地声速。

大气模型的参数包括空气密度ρ(单位：kg/m³)和当地声速V_s(单位：米每秒)；

ρ=1.2353×e-1.06×10-4hVs=340.63-4.076×10-3h]]>

h为导弹所处的飞行高度(单位：米)；

步骤二、根据导弹气动参数和大气模型的参数建立导弹运动方程组；

导弹运动方程组如下：

dVdt=-g sinθ-Dmdθdt=-g cosθV+LmVdxdt=V cosθdhdt=V sinθ]]>

其中，t为导弹的飞行时间，θ为弹道倾角，x为导弹的水平飞行距离，m为导弹质量，g为重力加速度；L和D分别为导弹的升力和导弹的阻力，计算式如下：

L=L(V,α,h)=12ρV2CLSD=D(V,α,h)=12ρV2CDS]]>

S是导弹的参考面积。

步骤三、对导弹运动方程组进行线性化处理，得到线性化处理方程组；

导弹运动方程组的线性化处理包含：

(1)引入法向加速度a_n：an=Lm-g cosθ;]]>

(2)设升阻比K为常数：

(3)将速度简化处理：将导弹运动方程组中导弹的实时速度V设为常数V₀；

(4)引入剩余时间：导弹的飞行时间t替换为剩余飞行时间t_go，t_go与t的关系如下：

t_go＝t_f-t

t_f为导弹的总飞行时间；

得到线性化处理方程组：

dVdtgo=an+gK+gθdθdtgo=-anV0dxdtgo=-V0dhdtgo=-V0θ]]>

步骤四、将线性化处理方程组中加入法向加速度导数方程，得到解析求解方程组；

法向加速度一阶导数方程为： 法向加速度二阶导数方程为：

其中 为法向加速度的一阶导数， 为法向加速度的二阶导数。

解析求解方程组如下：

dVdtgo=an+gK+gθdθdtgo=-anV0dxdtgo=-V0dhdtgo=-V0θdandtgo=-a·nda·ndtgo=-a··n=-u]]>

最后一式中的 表示把 当作控制量；

步骤五、导弹下滑时确定下滑段弹道要满足的末端约束和路径约束；

末端约束是指导弹在下滑段末端点要满足的约束；包括末端高度约束、速度约束、弹道倾角约束、法向加速度约束和末端法向加速度一阶导数约束；

具体设置如下：

h(t0)=h0h(tf)=hfθ(t0)=0θ(tf)=0x(t0)=0x(tf)=freeV(t0)=V0V(tf)=Vfan(t0)=an0an(tf)=anfa·n(t0)=a·n0a·n(tf)=a·nf]]>

其中，h(t₀)＝h₀表示t＝t₀时刻的高度为h₀，h(t_f)＝h_f表示在t＝t_f时刻的高度为h_f，θ(t₀)＝0表示t＝t₀时刻的弹道倾角为0；θ(t_f)＝0表示t＝t_f时刻的弹道倾角为0，x(t₀)＝0表示t＝t₀时刻导弹的水平飞行距离为0，x(t_f)＝free表示t＝t_f时刻导弹的水平飞行距离无约束，V(t₀)＝V₀表示t＝t₀时刻导弹相对大气的速度为常数V₀，V(t_f)＝V_f表示t＝t_f时刻导弹相对大气的速度为V_f，a_n(t₀)＝a_n0表示t＝t₀时刻导弹法向加速度为a_n0，a_n(t_f)＝a_nf表示t＝t_f时刻导弹法向加速度为a_nf， 表示t＝t₀时刻法向加速度的一阶导数为 表示t＝t_f时刻法向加速度的一阶导数为

路径约束主要包括导弹的速度和法向加速度约束，具体数学表达形式如下：

Vmin≤V≤Vmaxanmin≤an≤anmax]]>

其中V_min，V_max，a_nmin和a_nmax根据具体导弹的设计参数决定。

步骤六、选取最优控制的指标函数，根据解析求解方程组和指标函数确定最优控制量u；

选取能量控制为指标函数J：

J=∫0tf12u2dtgo]]>

控制量u控制导弹下滑段弹道平滑，缩短下滑段时间。

步骤七、求解最优控制量u得到解析制导律，使导弹下滑段弹道满足末端约束和路径约束。

基于最优控制理论中的极小值原理，对最优控制问题进行解析求解，得到解析制导律为：

u＝16x₁-120x₂+480x₃-840x₄

其中，x1=-a·n-a·nfτgo;x2=an-a·nfτgo-anfτgo2;x3=-Vθ+a·nfτgo22-anfτgoτgo2,]]>

x4=h-hf+a·nfτgo36-anfτgo22τgo4]]>

τgo=Kg(V-Vf)+Vgθ+KV(h-hf)]]>

τ_go是剩余飞行时间，物理意义与t_go相同，τ_go是在t_go的表达式中将参数V₀替换为V之后得到的。

本发明的优点与积极效果在于：

(1)一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，提出的导律与已有制导律相比，通过改变初始法向加速度来调节下滑段飞行时间，满足不同的任务需求。

(2)一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法，提出的导律与已有制导律相比，能够人为改变初始法向加速度，并且对末端法向加速度导数施加约束，使得弹道在初期下滑幅度较大，末端拉起弹道更平缓，更好地实现了下滑段快速下降和末端平稳拉起的要求。

附图说明

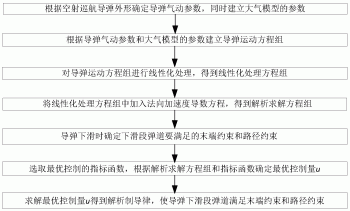
图1是本发明的设计流程图；

图2是战斧巡航导弹的外形图；

图3是解析解在不同投放高度下的弹道曲线示意图；

图4是解析解在不同投放高度下的速度曲线示意图；

图5是解析解在不同投放高度下的弹道倾角曲线示意图；

图6是解析解在不同投放高度下的曲线示意图；

图7是解析解在不同投放高度下的法向加速度曲线示意图；

图8是解析解在不同投放高度下的法向加速度一阶导数曲线示意图；

图9是解析解在不同投放高度下的升阻比曲线示意图；

图10是解析解与最优解的弹道曲线对比示意图；

图11是解析解与最优解的速度曲线对比示意图；

图12是解析解与最优解的弹道倾角曲线对比示意图；

图13是解析解与最优解的法向加速度曲线对比示意图；

图14是解析解与最优解的攻角曲线对比示意图；

图15是解析解与最优解的法向加速度一阶导数曲线对比示意图；

图16是解析解与最优解的升阻比曲线对比示意图；

图17是本发明与现有技术的弹道平滑度的对比示意图；

图18是本发明与现有技术的飞行时间对比示意图。

具体实施方式

下面将结合附图对本发明作进一步的详细说明。

基于最优控制的显式制导策略是解决下滑段制导问题的最新方法，主要包括广义显式制导律、分段最优制导律等，具有适应性强、鲁棒性好的特点；本发明在最优控制的显式制导策略基础上，采用在运动方程中加入法向加速度及其导数方程，引入法向加速度及其一阶导数约束，并用解析法求解，基于最优控制理论，使用最优控制模型解决了空射巡航导弹下滑段要满足末端约束的控制问题，在多约束制导律基础上，加入法向加速度一阶导数约束，能同时满足终端高度、速度、弹道倾角、法向加速度和法向加速度一阶导数约束的多约束制导律。

最优控制的相关理论如下：

最优控制属于变分法的范畴，系统的运动用以下非线性微分方程组来描述：

x·=f[x(t),u(t),t]---(1)]]>

其中，f[x(t),u(t),t]表示f是一个x(t),u(t)和t的非线性函数。

状态函数x(t)＝(x₁,x₂,…,x_n)是n维向量函数，控制函数u(t)＝(u₁,u₂,…,u_n)是m维的向量函数。

最优控制要解决的问题就是找到最优的控制函数u(t)，使得性能指标函数J最小：

J=φ[x(tf),tf)]+∫t0tfL[x(t),u(t),t]dt---(2)]]>

其中，L[x(t),u(t

一种包含法向加速度导数的空射巡航弹下滑段多约束制导方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。