专利摘要

专利摘要

本发明公开了一种充分灌溉条件下直接补渠的多库—多站系统水资源优化配置方法，采用“多库—多站”大系统分解—直接补渠的“单库—多站”子系统逆序动态规划逐次逼近优化—“补渠泵站群”二级子系统分解‑动态规划聚合的求解方法，可获得一定供水期内所有受水区最小缺水量、对应的各水库各时段最优供水量、弃水量、外调水量，以及各补渠泵站补水量过程。本发明对平原水库灌区水资源优化配置具有重要理论意义和实际应用价值。

权利要求

1.一种充分灌溉条件下直接补渠的多库-多站系统水资源优化配置方法，由多个补渠泵站向单水库所在供水渠道供水，形成一个直接补渠的单库-多站系统，再由多个串联的单库-多站系统构成直接补渠的多库-多站系统，联合向多个受水区供水，其特征在于，水资源优化配置方法包括以下步骤：

一、模型构建，包括以下步骤1～步骤2：

1.以直接补渠的多库-多站系统年内各时段的各水库供水量与受水区需水量之差的平方和最小为目标，建立如下目标函数：

F=min Z=minΣh=1RΣi=1N(Gh,i+Σk=1MYBh,k,i-YSh.i)2---(1)

式中：F为研究对象年内各时段的供需水量之差的最小平方和；Z为研究对象年内各时段的供需水量之差的平方和；R为水库数量，单位：座；h为水库编号，h＝1，2，......R；N为年内划分的时段数；i为时段编号，i＝1，2，......N；G_h，i、YS_h，i分别为第h座水库第i时段的供水量和对应的受水区第i时段的需水量，单位：万m³；YB_h，k，i为第h座水库所在供水渠道第k座补渠泵站第i时段供水量，单位：万m³；目标函数采用平方和表达是为了加速减少水库供水量与受水区需水量之间的偏差。

2.设置约束条件

包括直接补渠的单库-多站系统年可供水总量约束条件，考虑上级水库调入与自身外调水量要求的单水库水量平衡约束条件，单水库库容约束条件，以及补渠泵站群运行能耗最小约束条件。

二、模型求解

1.数据准备，具体包括：将1年划分为N个时段，并确定各时段长度；测定各水库初始库容V_h，0；确定各水库年可供水总量SK_h、死库容V_h，min、防洪限制水位对应的库容V_h，P、以及兴利库容V_h，min+Δ_h，1；测量和计算各水库各时段来水量LS_h，i、蒸发与渗漏量EF_h，i，h＝1，2，…R；确定各补渠泵站年允许提水总量BZ_h，k，k＝1，2，…M；测定不同时段扬程H_h，k，i下运行的提水流量Q_h，k，i及对应的η_{z，h，k，i}、η_mot，h，k、η_int，h，k；确定各时段各受水区的作物需水量YS_h，i，h＝1，2，......R；i＝1，2，…，N。

2.将直接补渠的“多库-多站”大系统模型分解为R个直接补渠的单库-多站水资源优化配置数学模型，目标函数为：

Fh=min Zh=minΣi=1N(Gh,i+Σk=1MYBh,k,i-YSh,i)2---(14)

3.对直接补渠的单库-多站水资源优化配置数学模型进行优化，从末级无外调水量要求的单库-多站系统出发，依次进行单库-多站系统水资源优化配置，具体包括：

(1)利用动态规划逐次逼近对单座水库-多站系统水资源优化配置子模型求解，获得的水库供水量过程G_h，i和泵站群补渠总水量过程Y_h，i作为原模型最优解，同时还获得目标函数最优值，水库最优弃水量过程PS_h，i，以及上一级水库对其的补库水量过程BK_h，i，其中，h＝1，…R；i＝1，…N。

(2)利用分解-动态规划聚合方法对补群泵站群二级子系统模型求解，获得满足第i时段泵站群目标提水总量Y_h，i的L_h，i值，以及对应的各泵站最优补水量组合YB_h，k，i^*k＝1，2，…M。

4.获得多水库-多泵站系统中每个水库各时段供水量G_h，i、外调水量WD_h，i、弃水量PS_h，i、上一级水库最优补库水量BK_h，i，以及对应的各补渠泵站补水量YB_h，k，i过程，h＝1，2，…，R。

2.根据权利要求1所述的方法，其特征在于，步骤(一)中的约束条件包括：

(1)直接补渠的单库-多站系统年可供水总量约束条件：除末级水库仅需向所在受水区供水外，其余各级水库还需承担外调水任务，供给下一级水库，即：

对第1～第R-1座水库：

Σi=1NΣk=1MYBh,k,i≤Σk=1MBZh,k---(3)

其中，h＝1，2，......R-1。

对第R座水库：

Σi=1NΣk=1MYBR,k,i≤Σk=1MBZR,k---(5)

式中：WD_h，i为第h座水库第i时段外调给下一级水库的供水量，单位：万m³；SK_h为第h座水库的年可供水总量，单位：万m³；M为第h座水库所在供水渠道的补渠泵站数量，单位：座；k为补渠泵站编号，k＝1，2，......M；BZ_h，k为第h座水库所在供水渠道的第k座补渠泵站年允许提水总量，单位：万m³。

(2)考虑上级水库调入与自身外调水量要求的单水库水量平衡约束条件：对于任意第h个多泵站直接补渠的单库-多站系统，考虑上级水库调入水量和水库本身外调水量要求，包括：对第1座水库，只有外调水量要求；对第2～R-1座水库，既有上级水库对其的补库水量，又有自身外调水量要求；对第R座水库，只有上级水库补库水量要求，即根据水量平衡方程：

对第1座水库：

V_1，i＝V_1，i-1+LS_1，i-PS_1，i-EF_1，i-G_1，i-WD_1，i (6)

对第2～第R-1座水库：

V_h，i＝V_h，i-1+LS_h，i+BK_h，i-PS_h，i-EF_h，i-G_h，i-WD_h，i (7)

其中，h＝2，3，…，R-1。

对第R座水库：

V_R，i＝V_R，i-1+LS_R，i+BK_R，i-PS_R，i-EF_R，i-G_R，i(8)

在此基础上，水库调度准则如下：

①当第i时段末水库蓄水量低于水库死库容V_h，min时，则第i时段应由上一级水库进行补水，补水至兴利库容，即：

V_h，i＜V_h，min时：BK_h，i＝V_h，min-V_h，i+Δ_h，1， (9)

此时段水库弃水PS_h，i＝0；h＝2，3，......R。

②当遭遇洪水，第i时段末水库蓄水量大于防洪限制水位所对应水库蓄水量V_h，P时，则第i时段应对水库进行弃水，弃水至水库防洪限制水位，即：

V_h，i＞V_h，P时：PS_h，i＝V_h，i-V_h，P (10)

此时段无需上一级水库调水，即BK_h，i＝0。

③当第i时段末水库蓄水量介于死库容V_h，min与防洪限制水位所对应水库蓄水量V_h，P之间，则第i时段水库不需要弃水，不需要上一级水库调水，即：

V_h，min≤V_h，i≤V_h，P时：PS_h，i＝BK_h，i＝0(11)

式中：V_h，i、V_h，i-1分别为第h座水库第i、i-1时段末的蓄水量，单位：万m³；LS_h，i、PS_h，i、EF_h，i分别为第h座水库第i时段的来水量、弃水量、蒸发与渗漏量，单位：万m³；BK_h，i为第h座水库第i时段由上一级，即第h-1座水库提供的补库水量，单位：万m³。

(3)单水库库容约束条件：各时段的水库蓄水量应介于水库死库容和防洪限制水位对应库容之间，即：

V_h，min≤V_h，i≤V_h，P，i＝1，2，…，N(12)

(4)补渠泵站群联合运行能耗最小约束条件：对任意第h座水库所在供水渠道的补渠泵站群，其在每一供水时段内的联合运行应考虑能耗最小，即：

Lh,i=Σk=1Mlh,k,i=Σk=1MρgQh,k,iHh,k,i1000ηz,h,k,iηmot,h,kηint,h,kΔTh,k,i=min---(13)

式中，L_h，i为第h座水库所在供水渠道第i时段补渠泵站群联合运行系统能耗，单位：kW·h；l_h，k，i为第h座水库所在供水渠道的第k座泵站第i时段运行能耗，单位：kW·h；M为第h座水库所在供水渠道的补渠泵站数量，单位：座；ρ为水密度，单位：kg/m³，g为重力加速度，单位：m/s²；Q_h，k，i、H_h，k，i、ΔT_h，k，i、η_{z，h，k，i}分别为第h座水库所在供水渠道的第k座泵站第i时段的流量(m³/s)、时均扬程(m)、时段长度(h)和水泵效率；η_mot，h，k、η_int，h，k分别为第h座水库所在供水渠道的第k座泵站的电动机效率和传动效率。

3.根据权利要求1所述的方法，其特征在于，步骤(二)中，单个直接补渠的单库-多站水资源优化配置数学模型的约束条件如下：

(1)直接补渠的单库-多站系统年可供水总量约束：

①对于第1～第R-1座水库，除向受水区供水外，还有外调给下级水库的供水量要求，因此：

Σi=1N(Gh,i+WDh,i)≤SKh---(15)

Σi=1NΣk=1MYBh,k,i≤Σk=1MBZh,k---(16)

式中，h＝1，2，......R-1。

②对于第R座水库，仅向受水区供水，无外调给下级水库的供水量要求，因此：

Σi=1NGR,i≤SKR---(17)

Σi=1NΣk=1MYBR,k,i≤Σk=1MBZR,k---(18)

(2)考虑上级水库调入与自身外调水量要求的单水库水量平衡约束条件：

①对第1座水库：

V_1，i＝V_1，i-1+LS_1，i-PS_1，i-EF_1，i-G_1，i-WD_1，i(19)

②对第2～第R-1座水库：

V_h，i＝V_h，i-1+LS_h，i+BK_h，i-PS_h，i-EF_h，i-G_h，i-WD_h，i (20)

其中，h＝2，3，…，R-1。

③对第R座水库：

V_R，i＝V_R，i-1+LS_R，i+BK_R，i-PS_R，i-EF_R，i-G_R，i (21)

在此基础上的水库调度准则同式(9)～(11)。

(3)单水库库容约束条件：同式(12)。

(4)补渠泵站群联合运行能耗最小约束条件：同式(13)。

4.根据权利要求1所述的方法，其特征在于，步骤(二)的第3步具体步骤如下：

(1)第R座单库-多站系统水资源优化配置子模型求解

1)子模型转换

对于子模型(14)～(21)、(9)～(13)，取 则子模型转换为以水库各阶段供水量G_R，i、补渠泵站群各阶段补水总量Y_R，i为决策变量的二维非线性数学模型，即：

目标函数：

FR=min ZR=minΣi=1N(GR,i+YR,i-YSR,i)2---(22)

单库-多站系统年可供水总量约束条件：

Σi=1NGR,i≤SKR---(23)

Σi=1NYBR,i≤Σk=1MBZR,k---(24)

水库水量平衡约束条件：

V_R，i＝V_R，i-1+LS_R，i+BK_R，i-PS_R，i-EF_R，i-G_R，i (25)

在此基础上，水库调度准则条件为：

①当第i时段末水库蓄水量低于水库死库容V_R，min时，则第i时段应由上一级水库进行补水，补水至兴利库容，即：

V_R，i＜V_R，min时：BK_R，i＝V_R，min-V_R，i+Δ_R，1(26)

此时段水库弃水PS_R，i＝0。

②当遭遇洪水，第i时段末水库蓄水量大于防洪限制水位所对应水库蓄水量V_R，P时，则第i时段应对水库进行弃水，弃水至水库防洪限制水位，即：

V_R，i＞V_R，P时：PS_R，i＝V_R，i-V_R，P (27)

此时段无需上一级水库调水，即BK_R，i＝0。

③当第i时段末水库蓄水量介于死库容V_R，min与防洪限制水位所对应水库蓄水量V_R，P之间，则第i时段水库不需要弃水，不需要上一级水库调水，即：

V_R，min≤V_R，i≤V_R，P时：PS_R，i＝BK_R，i＝0 (28)

其余约束同式(12)～(13)。

2)子模型动态规划逐次逼近求解

针对转换模型(22)～(28)、(12)～(13)，动态规划逐次逼近求解具体步骤如下：

①以常规水库阶段供水量过程G_R，i，1作为初始迭代值，将其代入式(22)，则子模型(22)～(28)、(12)～(13)转化为以各阶段泵站群补渠总水量Y_R，i为决策变量，前i个阶段泵站群补水总量λ_i为状态变量的一维动态规划模型，采用一维动态规划法求解；其中，i＝1，2，......N。

②参照一维动态规划求解原理，得对应递推方程为：

i)阶段i＝1：

g₁(λ₁)＝min(G_R，1，1+Y_R，1，1-YS_R，1)²(29)

该时段水库供水量G_R，1，1已由初始值给定，状态变量λ₁，其在对应可行域内离散： 对每个离散的λ₁，泵站群补水总量Y_R，1，1在对应可行域内离散，应满足：Y_R，1，1≥λ₁。将满足要求的Y_R，1，1分别代入式(29)，分别得到对应于每个离散λ₁值时，最优Y_R，1，1及其对应的该时段最小缺水量平方和g₁(λ₁)。

而后，根据式(25)，第1阶段末水库库容V_R，1＝V_R，0+LS_R，1-EF_R，1-G_R，1，1，此时尚未考虑上一级水库补水和水库弃水，采用式(26)～(28)检验：

a、当V_R，1＜V_R，min，则考虑由上一级水库对其补水，补库水量BK_R，1，1＝V_R，min-V_R，1+Δ_R，1，此时修正库容V_R，1^*＝V_R，min+Δ_R，1。

b、当V_R，1＞V_R，P，则需要弃水来保证水库库容的调度需求，PS_R，1，1＝V_R，1-V_R，P，此时修正库容V_R，1^*＝V_R，P。

c、当V_R，min≤V_R，1≤V_R，P，则BK_R，1，1＝PS_R，1，1＝0，此时修正库容V_R，1^*＝V_R，1。

通过步骤a～c，修正并确定第1阶段末水库库容V_R，1^*，同时可获得对应的水库弃水量PS_R，1，1、或上一级水库补库水量BK_R，1，1。

ii)阶段i＝2，3，…N-1：

g_i(λ_i)＝min[(G_R，i，1+Y_R，i，1-YS_R，i)²+g_i-1(λ_i-1)](30)

该时段水库供水量G_R，i，1已由初始值给定，状态变量λ_i同样分别进行离散： 对每个离散的λ_i，泵站群补水总量Y_R，i，1离散应满足：

状态转移方程：

式中：i＝2，3，...，N-1。

对每个离散的λ_i，将各离散的Y_R，i，1值分别代入式(30)中的(G_R，i，1+Y_R，i，1-YS_R，i)²，由状态转移方程式(31)，查找i-1阶段满足 要求的g_i-1(λ_i-1)值，由此获得满足该λ_i要求的最优Y_R，i，1过程及其对应的前i个时段子系统最小缺水量平方和g_i(λ_i)。同样，根据式(25)，第i时段末水库库容V_R，i＝V_R，i-1+LS_R，i-EF_R，i-G_R，i，1，此时尚未考虑上一级水库补水和水库弃水，同样按照式(26)～(28)，采用上述步骤a～c进行检验，修正并确定第i阶段末水库库容V_R，i^*，同时可获得对应的水库弃水量PS_R，i，1、或上一级水库补库水量BK_R，i，1，其中，i＝1，2，...，i。

iii)阶段N：

g_N(λ_N)＝min[(G_R，N，1+Y_R，N，1-YS_R，N)²+g_N-1(λ_N-1)](32)

该时段水库供水量G_R，N，1已由初始值给定，状态变量 决策变量泵站群补水总量Y_R，N，1同样在对应可行域内离散，应满足：λ_N-1＝λ_N-(YS_R，N-G_R，N，1)。

采用步骤ii)所述方法，最终获得满足该λ_N要求的泵站群最优补水总量过程Y_R，i，1，对应的水库弃水量过程PS_R，i，1，以及上一级水库对其的补库水量过程BK_R，i，1，其中，i＝1，…N。

③将步骤②获得的泵站群补渠总水量过程Y_R，i，1作为初始给定值，代入式(22)，则子模型(22)～(28)、(12)～(13)又转化为以各阶段水库供水量G_R，i为决策变量，前i个阶段水库供水总量λ_i′为状态变量的一维动态规划模型，参照步骤②，采用一维动态规划法求解，获得满足该λ_N′要求的水库最优供水过程G_R，i，2(i＝1，…N)，对应的水库弃水量过程PS_R，i，2，以及上一级水库对其的补库水量过程BK_R，i，2，其中，i＝1，…N。

④将步骤③获得的水库供水量过程G_R，i，2作为初始给定值，代入式(22)，重复步骤②～③，反复逐次逼近求解，直到相邻两次目标函数最优值误差精度小于要求的迭代控制精度ε，则子模型优化结束。以最后一次优化获得的水库供水量过程G_R，i，m和泵站补渠总水量过程Y_R，i，m作为原模型最优解，同时还可获得目标函数最优值，水库最优弃水量过程PS_R，i，m，以及上一级水库对其的补库水量过程BK_R，i，m。其中，i＝1，…N；m为动态规划逐次逼近迭代次数编号。

3)“补渠泵站群”二级子系统模型分解-动态规划聚合方法求解

①补渠泵站群子系统经济运行数学模型构建

考虑补水泵站群联合运行能耗最小准则约束条件，由式(13)建立补渠泵站群经济运行数学模型：

目标函数：

时段供水量约束：

功率约束：

式中，N_R，k，0为第R座水库所在供水渠道的第k座补渠泵站的电机配套功率(kW)。

gN(λN)=min[(GR,N,1+YR,N,1-YSR,N)2+gN-1(λN-1)]---(32)

该时段水库供水量G_R，N，1已由初始值给定，状态变量 决策变量泵站群补水总量Y_R，N，1同样在对应可行域内离散，应满足：λ_N-1＝λ_N-(YS_R，N-G_R，N，1)。

采用步骤ii)所述方法，最终获得满足该λ_N要求的泵站群最优补水总量过程Y_R，i，1，对应的水库弃水量过程PS_R，i，1，以及上一级水库对其的补库水量过程BK_R，i，1，其中，i＝1，…N。

③将步骤②获得的泵站群补渠总水量过程Y_R，i，1作为初始给定值，代入式(22)，则子模型(22)～(28)、(12)～(13)又转化为以各阶段水库供水量G_R，i为决策变量，前i个阶段水库供水总量λ_i′为状态变量的一维动态规划模型，参照步骤②，采用一维动态规划法求解，获得满足该λ_N′要求的水库最优供水过程G_R，i，2(i＝1，…N)，对应的水库弃水量过程PS_R，i，2，以及上一级水库对其的补库水量过程BK_R，i，2，其中，i＝1，…N。

④将步骤③获得的水库供水量过程G_R，i，2作为初始给定值，代入式(22)，重复步骤②～③，反复逐次逼近求解，直到相邻两次目标函数最优值误差精度小于要求的迭代控制精度ε，则子模型优化结束。以最后一次优化获得的水库供水量过程G_R，i，m和泵站补渠总水量过程Y_R，i，m作为原模型最优解，同时还可获得目标函数最优值，水库最优弃水量过程PS_R，i，m，以及上一级水库对其的补库水量过程BK_R，i，m。其中，i＝1，…N；m为动态规划逐次逼近迭代次数编号。

3)“补渠泵站群”二级子系统模型分解-动态规划聚合方法求解

①补渠泵站群子系统经济运行数学模型构建

考虑补水泵站群联合运行能耗最小准则约束条件，由式(13)建立补渠泵站群经济运行数学模型：

目标函数：

时段供水量约束：

功率约束：

式中，N_R，k，0为第R座水库所在供水渠道的第k座补渠泵站的电机配套功率(kW)。型，获得满足第i时段泵站目标提水总量Y_R，i的L_R，i值，以及对应的各泵站最优补水量组合YB_R，k，i^*，k＝1，2，…M。

4)确定第R座单库-多站系统子模型最优解

通过步骤2)获得的各时段补渠泵站群最优补水总量Y_R，i，i＝1，2，......N后；对每个时段确定的Y_R，i，均需经由一次步骤3)计算，共N次步骤3)，将各时段Y_R，i优化分配至M个补渠泵站，获得各补渠泵站各时段最优补水量YB_R，k，i^*；由此最终获得第R级单库-多站系统年内各时段的供需水量之差的最小平方和F_R、对应的水库各时段最优供水量G_R，i、弃水过程PS_R，i、上一级水库对其的补库水量BK_R，i，以及各补渠泵站各时段最优补水量过程YB_R，k，i^*，i＝1，2，......N，k＝1，2，…M。

(2)第R-1，R-2，…，1座单库-多站系统水资源优化配置子模型求解

对于第R-1，R-2，…，1座直接补渠的单库-多站系统，同样采用子模型(14)～(21)、(9)～(13)，是以水库各时段供水量G_R，i、该水库所在供水渠道各补渠泵站各时段补水量YB_R，k，i为决策变量的M+1维非线性模型，参照步骤(1)，取 则该子模型转换为以水库各阶段供水量G_h，i、补渠泵站群各阶段补水总量Y_h，i为决策变量的二维非线性数学模型，仍采用动态规划逐次逼近法求解。区别仅在于：

1)直接补渠的单库-多站系统年可供水总量约束条件：

单库-多站系统年可供水总量约束应采用式(15)～(16)，即： 以及 由于采用逆序法，其外调水量WD_h，i即下一级单库-多站系统的补库水量BK_h+1，i，其已由前一次单库-多站系统优化过程中的水库调度准则确定，即：

WD_h，i＝BK_h+1，i(40)

则式(15)可以转化为如下式(41)，从而获得水库供水量约束范围。

Σi=1N(Gh,i+BKh+1,i)≤SKh---(41)

2)满足外调水量和上级水库补库水量要求的单水库调度准则约束：

对各阶段水量平衡方程应考虑本水库外调水量WD_h，i，以及上一级水库对其的补库水量BK_h，i两方面因素，应分别考虑：对第1座水库，应采用式(19)，即：V_1，i＝V_1，i-1+LS_1，i-PS_1，i-EF_1，i-G_1，i-WD_1，i；对第2～第R-1座水库，应采用式(20)，即：V_h，i＝V_h，i-1+LS_h，i+BK_h，i-PS_h，i-EF_h，i-G_h，i-WD_h，i。

同理，由式(40)，可将式(19)～(20)转化如下形式：

①对第1座水库，

V_1，i＝V_1，i-1+LS_1，i-PS_1，i-EF_1，i-G_1，i-BK_2，i(42)

②对第2～第R-1座水库，

V_h，i＝V_h，i-1+LS_h，i+BK_h，i-PS_h，i-EF_h，i-G_h，i-BK_h+1，i (43)

在此基础上，仍采用式(9)～(11)对各阶段库容进行修正。

说明书

技术领域

本发明涉及充分灌溉条件下梯级水库群与多个补渠泵站群联合运行调度的方法，属于灌区水资源优化配置技术领域。

背景技术

当前由于水资源时空分布不均，已制约不少地区的经济社会发展，对于充分灌溉条件的灌区而言，在有限水资源总量和水源工程规模下，以用水综合效益最大为目标，加强区域水资源的统一调度和管理，把灌溉系统的水利工程作为统一整体来运用和调节，运用已建工程(如多个水库群和多个泵站群联合调度运行)使其发挥更大的作用，是解决灌区缺水问题的主要途径。多水库—多泵站系统运行调度作为水资源管理一项内容，如何合理地运用系统水资源调度达到某个目标使系统效益最佳，是水利工程管理中较为常见的问题。

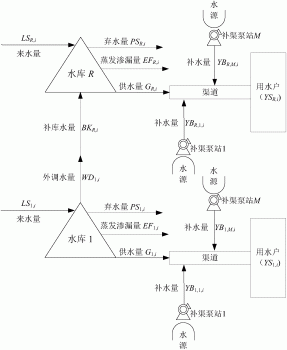
对于直接补渠的多库—多站系统水资源优化配置，由多个补渠泵站向单水库供水渠道供水，形成一个直接补渠的单库—多站系统，再由多个串联的单库—多站系统构成直接补渠的多库—多站系统，联合向多个受水区供水。虽然水源条件充分，但由于涉及多个水库群，在系统实际运行时，除末级单库—多站系统仅向受水区供水外，其余各级单库—多站系统还附加外调给下一级单库—多站系统的供水量；且对每一个单库—多站系统而言，又包含多个补渠泵站群，如何在保证受水区供水充分的条件下，降低补渠泵站群系统运行能耗，节约工程运行成本，是不可忽视的重要问题。

发明内容

本发明针对特定的年调节多水库—多泵站联合运行调度系统，在已知水库供水划分的时段数、水库数量、各水库的初始库容、死库容、兴利库容、防洪限制水位对应的库容、年可供水总量、各时段来水量过程、蒸发与渗漏量过程，各水库补渠泵站数量、各补渠泵站年允许提水总量，以及各时段各受水区需水量过程情况下，采用“多库—多站”大系统分解—直接补渠的“单库—多站”子系统逆序动态规划逐次逼近优化—“补渠泵站群”二级子系统分解-动态规划聚合的求解方法，可获得一定供水期内受水区最小缺水量、对应的各水库供水期内各时段最优供水量、弃水量、外调水量，以及各补渠泵站各时段补水量过程。

本发明方案如下：

一种充分灌溉条件下直接补渠的多库—多站系统水资源优化配置，由多个补渠泵站向单水库所在供水渠道供水，形成一个直接补渠的单库—多站系统，再由多个串联的单库—多站系统构成直接补渠的多库—多站系统，联合向多个受水区供水。其水资源优化配置方法包括以下步骤：

一、模型构建，包括以下步骤1～步骤2：

1.以直接补渠的多库—多站系统年内各时段的各水库供水量与受水区需水量之差的平方和最小为目标，建立如下目标函数：

式中：F为研究对象年内各时段的供需水量之差的最小平方和；Z为研究对象年内各时段的供需水量之差的平方和；R为水库数量，单位：座；h为水库编号，h＝1,2,……R；N为年内划分的时段数；i为时段编号，i＝1,2,……N；G_h,i、YS_h,i分别为第h座水库第i时段的供水量和对应的受水区第i时段的需水量，单位：万m³；YB_h,k,i为第h座水库所在供水渠道第k座补渠泵站第i时段供水量，单位：万m³；目标函数采用平方和表达是为了加速减少水库供水量与受水区需水量之间的偏差。

2.设置约束条件

包括直接补渠的单库—多站系统年可供水总量约束条件，考虑上级水库调入与自身外调水量要求的单水库水量平衡约束条件，单水库库容约束条件，以及补渠泵站群运行能耗最小约束条件。

二、模型求解

1.数据准备，具体包括：将1年划分为N个时段，并确定各时段长度；测定各水库初始库容V_h,0；确定各水库年可供水总量SK_h、死库容V_h,min、防洪限制水位对应的库容V_h,P、以及兴利库容V_h,min+Δ_h,1；测量和计算各水库各时段来水量LS_h,i、蒸发与渗漏量EF_h,i，h＝1,2,…R；确定各补渠泵站年允许提水总量BZ_h,k，k＝1,2,…M；测定不同时段扬程H_h,k,i下运行的提水流量Q_h,k,i及对应的水泵效率η_z,h,k,i、电机效率η_mot,h,k、传动效率η_int,h,k；确定各时段各受水区的作物需水量YS_h,i，h＝1,2,……R；i＝1,2,…,N。

2.将直接补渠的“多库—多站”大系统模型分解为R个直接补渠的单库—多站水资源优化配置数学模型，目标函数为：

3.对直接补渠的单库—多站水资源优化配置数学模型进行优化，从末级无外调水量要求的单库—多站系统出发，依次进行单库—多站系统水资源优化配置，具体包括：

(1)利用动态规划逐次逼近对单座水库—多站系统水资源优化配置子模型求解，获得的水库供水量过程G_h,i和泵站群补渠总水量过程Y_h,i作为原模型最优解，同时还获得目标函数最优值，水库最优弃水量过程PS_h,i，以及上一级水库对其的补库水量过程BK_h,i，其中， h＝1,…R；i＝1,…N。

(2)利用分解-动态规划聚合方法对补群泵站群二级子系统模型求解，获得满足第i时段泵站群目标提水总量Y_h,i的L_h,i值，以及对应的各泵站最优补水量组合YB_h,k,i^*k＝1,2,…M。

4.获得多水库-多泵站系统中每个水库各时段供水量G_h,i、外调水量WD_h,i、弃水量 PS_h,i、上一级水库最优补库水量BK_h,i，以及对应的各补渠泵站补水量YB_h,k,i过程，h＝1， 2，…，R。

进一步地，步骤(一)中的约束条件包括：

(1)直接补渠的单库—多站系统年可供水总量约束条件：除末级水库仅需向所在受水区供水外，其余各级水库还需承担外调水任务，供给下一级水库，即：

对第1～第R-1座水库：

其中，h＝1,2,……R-1。

对第R座水库：

式中：WD_h,i为第h座水库第i时段外调给下一级水库的供水量，单位：万m³；SK_h为第h 座水库的年可供水总量，单位：万m³；M为第h座水库所在供水渠道的补渠泵站数量，单位：座；k为补渠泵站编号，k＝1,2,……M；BZ_h,k为第h座水库所在供水渠道的第k座补渠泵站年允许提水总量，单位：万m³。

(2)考虑上级水库调入与自身外调水量要求的单水库水量平衡约束条件：对于任意第h个多泵站直接补渠的单库—多站系统，考虑上级水库调入水量和水库本身外调水量要求，包括：对第1座水库，只有外调水量要求；对第2～R-1座水库，既有上级水库对其的补库水量，又有自身外调水量要求；对第R座水库，只有上级水库补库水量要求，即根据水量平衡方程：

对第1座水库：

V_1,i＝V_1,i-1+LS_1,i-PS_1,i-EF_1,i-G_1,i-WD_1,i (6)

对第2～第R-1座水库：

V_h,i＝V_h,i-1+LS_h,i+BK_h,i-PS_h,i-EF_h,i-G_h,i-WD_h,i (7)

其中，h＝2,3,…,R-1。

对第R座水库：

V_R,i＝V_R,i-1+LS_R,i+BK_R,i-PS_R,i-EF_R,i-G_R,i (8)

在此基础上，水库调度准则如下：

①当第i时段末水库蓄水量低于水库死库容V_h,min时，则第i时段应由上一级水库进行补水，补水至兴利库容，即：

V_h,i＜V_h,min时：

此时段水库弃水PS_h,i＝0；h＝2,3,……R。

②当遭遇洪水，第i时段末水库蓄水量大于防洪限制水位所对应水库蓄水量V_h,P时，则第i时段应对水库进行弃水，弃水至水库防洪限制水位，即：

V_h,i＞V_h,P时：

此时段无需上一级水库调水，即BK_h,i＝0。

③当第i时段末水库蓄水量介于死库容V_h,min与防洪限制水位所对应水库蓄水量V_h,P之间，则第i时段水库不需要弃水，不需要上一级水库调水，即：

V_h,min≤V_h,i≤V_h,P时：PS_h,i＝BK_h,i＝0 (11)

式中：V_h,i、V_h,i-1分别为第h座水库第i、i-1时段末的蓄水量，单位：万m³；LS_h,i、PS_h,i、 EF_h,i分别为第h座水库第i时段的来水量、弃水量、蒸发与渗漏量，单位：万m³；BK_h,i为第h座水库第i时段由上一级，即第h-1座水库提供的补库水量，单位：万m³。

(3)单水库库容约束条件：各时段的水库蓄水量应介于水库死库容和防洪限制水位对应库容之间，即：

V_h,min≤V_h,i≤V_h,P，i＝1,2，···，N (12)

(4)补渠泵站群联合运行能耗最小约束条件：对任意第h座水库所在供水渠道的补渠泵站群，其在每一供水时段内的联合运行应考虑能耗最小，即：

式中，L_h,i为第h座水库所在供水渠道第i时段补渠泵站群联合运行系统能耗，单位： kW·h；l_h,k,i为第h座水库所在供水渠道的第k座泵站第i时段运行能耗，单位：kW·h；M为第 h座水库所在供水渠道的补渠泵站数量，单位：座；ρ为水密度，单位：kg/m³，g为重力加速度，单位：m/s²；Q_h,k,i、H_h,k,i、ΔT_h,k,i、η_z,h,k,i分别为第h座水库所在供水渠道的第k座泵站第i时段的流量(m³/s)、时均扬程(m)、时段长度(h)和水泵效率；η_mot,h,k、η_int,h,k分别为第h座水库所在供水渠道的第k座泵站的电动机效率和传动效率。

进一步地，步骤(二)中，单个直接补渠的单库—多站水资源优化配置数学模型的约束条件如下：

(1)直接补渠的单库—多站系统年可供水总量约束：

①对于第1～第R-1座水库，除向受水区供水外，还有外调给下级水库的供水量要求，因此：

式中，h＝1,2,……R-1。

②对于第R座水库，仅向受水区供水，无外调给下级水库的供水量要求，因此：

(2)考虑上级水库调入与自身外调水量要求的单水库水量平衡约束条件：

①对第1座水库：

②对第2～第R-1座水库：

V_h,i＝V_h,i-1+LS_h,i+BK_h,i-PS_h,i-EF_h,i-G_h,i-WD_h,i (20)

其中，h＝2,3,…,R-1。

③对第R座水库：

V_R,i＝V_R,i-1+LS_R,i+BK_R,i-PS_R,i-EF_R,i-G_R,i (21)

在此基础上的水库调度准则同式(9)～(11)。

(3)单水库库容约束条件：同式(12)。

(4)补渠泵站群联合运行能耗最小约束条件：同式(13)。

进一步地，步骤(二)的第3步具体步骤如下：

(1)第R座单库—多站系统水资源优化配置子模型求解

1)子模型转换

对于子模型(14)～(21)、(9)～(13)，取 则子模型转换为以水库各阶段供水量G_R,i、补渠泵站群各阶段补水总量Y_R,i为决策变量的二维非线性数学模型，即：

目标函数：

单库—多站系统年可供水总量约束条件：

水库水量平衡约束条件：

V_R,i＝V_R,i-1+LS_R,i+BK_R,i-PS_R,i-EF_R,i-G_R,i (25)

在此基础上，水库调度准则条件为：

①当第i时段末水库蓄水量低于水库死库容V_R,min时，则第i时段应由上一级水库进行补水，补水至兴利库容，即：

V_R,i＜V_R,min时：

此时段水库弃水PS_R,i＝0。

②当遭遇洪水，第i时段末水库蓄水量大于防洪限制水位所对应水库蓄水量V_R,P时，则第i时段应对水库进行弃水，弃水至水库防洪限制水位，即：

V_R,i＞V_R,P时：

此时段无需上一级水库调水，即BK_R,i＝0。

③当第i时段末水库蓄水量介于死库容V_R,min与防洪限制水位所对应水库蓄水量V_R,P之间，则第i时段水库不需要弃水，不需要上一级水库调水，即：

V_R,min≤V_R,i≤V_R,P时：PS_R,i＝BK_R,i＝0 (28)

其余约束同式(12)～(13)。

2)子模型动态规划逐次逼近求解

针对转换模型(22)～(28)、(12)～(13)，动态规划逐次逼近求解具体步骤如下：

①以常规水库阶段供水量过程G_R,i,1作为初始迭代值，将其代入式(22)，则子模型(22) ～(28)、(12)～(13)转化为以各阶段泵站群补渠总水量Y_R,i为决策变量，前i个阶段泵站群补水总量λ_i为状态变量的一维动态规划模型，采用一维动态规划法求解；其中， i＝1,2,……N。

②参照一维动态规划求解原理，得对应递推方程为：

ⅰ)阶段i＝1：

g₁(λ₁)＝min(G_R,1,1+Y_R,1,1-YS_R,1)² (29)

该时段水库供水量G_R,1,1已由初始值给定，状态变量λ₁，其在对应可行域内离散： 对每个离散的λ₁，泵站群补水总量Y_R,1,1在对应可行域内离散，应满足：Y_R,1,1≥λ₁。将满足要求的Y_R,1,1分别代入式(29)，分别得到对应于每个离散λ₁值时，最优Y_R,1,1及其对应的该时段最小缺水量平方和g₁(λ₁)。

而后，根据式(25)，第1阶段末水库库容V_R,1＝V_R,0+LS_R,1-EF_R,1-G_R,1,1，此时尚未考虑上一级水库补水和水库弃水，采用式(26)～(28)检验：

a、当V_R,1＜V_R,min，则考虑由上一级水库对其补水，补库水量BK_R,1,1＝V_R,min-V_R,1+Δ_R,1，此时修正库容V_R,1^*＝V_R,min+Δ_R,1。

b、当V_R,1＞V_R,P，则需要弃水来保证水库库容的调度需求，PS_R,1,1＝V_R,1-V_R,P，此时修正库容V_R,1^*＝V_R,P。

c、当V_R,min≤V_R,1≤V_R,P，则BK_R,1,1＝PS_R,1,1＝0，此时修正库容V_R,1^*＝V_R,1。

通过步骤a～c，修正并确定第1阶段末水库库容V_R,1^*，同时可获得对应的水库弃水量 PS_R,1,1、或上一级水库补库水量BK_R,1,1。

ⅱ)阶段i＝2，3，…N-1：

g_i(λ_i)＝min[(G_R,i,1+Y_R,i,1-YS_R,i)²+g_i-1(λ_i-1)] (30)

该时段水库供水量G_R,i,1已由初始值给定，状态变量λ_i同样分别进行离散： 对每个离散的λ_i，泵站群补水总量Y_R,i,1离散应满足：

状态转移方程：

式中：i＝2，3，…，N-1。

对每个离散的λ_i，将各离散的Y_R,i,1值分别代入式(30)中的(G_R,i,1+Y_R,i,1-YS_R,i)²，由状态转移方程式(31)，查找i-1阶段满足 要求的g_i-1(λ_i-1)值，由此获得满足该λ_i要求的最优Y_R,i,1过程及其对应的前i个时段子系统最小缺水量平方和g_i(λ_i)。同样，根据式(25)，第i时段末水库库容V_R,i＝V_R,i-1+LS_R,i-EF_R,i-G_R,i,1，此时尚未考虑上一级水库补水和水库弃水，同样按照式(26)～(28)，采用上述步骤a～c进行检验，修正并确定第i 阶段末水库库容V_R,i^*，同时可获得对应的水库弃水量PS_R,i,1、或上一级水库补库水量BK_R,i,1，其中，i＝1，2，…，i

一种充分灌溉条件下直接补渠的多库-多站系统水资源优化配置方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。