专利摘要

本发明公开了一种变换炉系统的炉温控制方法，该方法包括依次执行的如下步骤：采集变换炉在某段时间内的输入数据和输出数据，构建一个基于数据的变换炉系统炉温模型，该模型利用神经网络构建变换炉系统动态特性，用于确定变换炉炉温变化情况；根据所采集的数据，利用三层BP神经网络构建参考控制模型，用于确定变换炉系统输入参考量；将构建的带有变换炉系统炉温模型误差和参考控制模型误差的最优跟踪控制问题，利用系统变换转化为最优调节器问题；基于迭代自适应动态规划最优控制方法，求解最优控制的函数，最终获得系统的最优控制。本发明能够高效、实时、最优化控制变换炉温度，实现变换炉系统最优化运行。

权利要求

1.一种变换炉系统的炉温控制方法，所述变换炉用于将原料中的CO和H₂O转化为CO₂和H₂，其中所述方法包括：

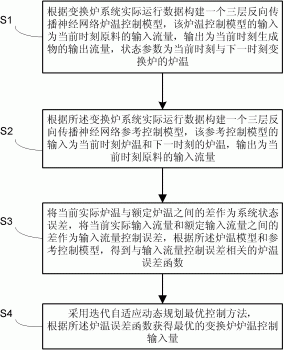
S1、根据变换炉系统实际运行数据构建一个三层反向传播神经网络炉温控制模型，该炉温控制模型的输入为当前时刻原料中CO、CO₂、H₂和H₂O的输入流量，输出为当前时刻生成物中CO、CO₂、H₂和H₂O的输出流量，状态参数为当前时刻与下一时刻变换炉的炉温；

S2、根据所述变换炉系统实际运行数据构建一个三层反向传播神经网络参考控制模型，该参考控制模型的输入为当前时刻炉温和下一时刻的炉温，输出为当前时刻原料中CO、CO₂、H₂和H₂O的输入流量；

S3、将当前实际炉温与额定炉温之间的差作为系统状态误差，将当前实际输入流量和额定输入流量之间的差作为输入流量控制误差，根据所述炉温模型和参考控制模型，得到与输入流量控制误差相关的炉温误差函数；

S4、基于迭代自适应动态规划最优控制方法，根据所述炉温误差函数求解出最优输入流量控制误差函数，获得最优的变换炉炉温控制输入量。

2.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，在步骤S1中构建的所述炉温控制模型表示为：

$\left\{\begin{array}{c}\hat{x}(k+1)=\hat{F}(x\left(k\right),u\left(k\right))={\hat{W}}_{m1}^T\left(k\right){\sigma }_1\left(z\left(k\right)\right)\\ \hat{y}\left(k\right)=\hat{G}(x\left(k\right),u\left(k\right))={\hat{W}}_{m2}^T\left(k\right){\sigma }_2\left(z\left(k\right)\right)\end{array}\right.,$

其中， 为神经网络系统函数， 为变换炉系统炉温模型的神经网络权值， 为变换炉系统输出模型的神经网络权值，z(k)=[x^T(k)，u^T(k)]^T为构建所述变换炉炉温系统模型使用的神经网络的输入， 为k+1时刻变换炉炉温系统模型的炉温值， 为k时刻变换炉炉温系统模型的输出，x(k)为k时刻实际的炉温，u(k)为k时刻实际的组分输入流量，σ(·)为训练系统控制模型使用的神经网络双极S型激活函数，如下表示：

${\left[\sigma \left(z\right)\right]}_i=\frac{e^{z_i}-e^{-z_i}}{e^{z_i}+e^{-z_i}}.$

3.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，在步骤S1中所述神经网络权值 和 通过如下训练更新得到：

$\left\{\begin{array}{c}{\hat{W}}_{m1}^{j+1}(k+1)={\hat{W}}_{m1}^j\left(k\right)-l_{m1}{\sigma }_1\left(z\left(k\right)\right){\tilde{x}}^{\mathrm{jT}}(k+1)\\ {\hat{W}}_{m2}^{j+1}(k+1)={\hat{W}}_{m2}^j\left(k\right)-l_{m2}{\sigma }_2\left(z\left(k\right)\right){\tilde{y}}^{\mathrm{jT}}\left(k\right)\end{array}\right.,$

其中，l_m1>0，l_m2>0为神经网络的学习率， 为k+1时刻根据所述变换炉炉温系统模型得到的炉温 和变换炉系统运行过程中测量得到的实际炉温的差值， 为k+1时刻根据所述变换炉炉温系统模型得到的输出 和变换炉系统运行过程中测量得到的实际输出y(k)的差值。

4.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，在步骤S2中所述参考控制模型如下所示：

${\hat{u}}_f\left(k\right)={\hat{F}}_u(x\left(k\right),x(k+1))={\hat{W}}_u^T\left(k\right){\sigma }_u\left(z_u\left(k\right)\right),$

其中， 表示参考控制模型的输出， 表示参考控制函数， 为参考控制模型神经网络权值，z_u(k)=[x^T(k)，x^T(k+1)]^T为参考控制模型输入，x(k)为k时刻的实际炉温，x(k+1)为k+1时刻的实际炉温，σ_u(·)为训练参考控制模型使用的神经网络双极S型激活函数，如下表示：

${\sigma }_u\left(z\right)=\frac{e^z-e^{-z}}{e^z+e^{-z}}.$

5.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，

在步骤S2中所述参考控制模型权值更新如下：

${\hat{W}}_u^{j+1}\left(k\right)={\hat{W}}_u^j\left(k\right)-l_u{\sigma }_u\left(z_u\left(k\right)\right){\tilde{u}}_f^j\left(k\right),$

其中，l_u>0为神经网络学习率， 为k时刻所述参考控制模型的输出 和变换炉系统运行过程中测量得到的实际输入量u(k)的差值。

6.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，在步骤S3中转化后的变换炉炉温使用如下所示的误差函数e(k)表示：

$\begin{array}{c}e(k+1)=\bar{F}(e\left(k\right),u_e\left(k\right))\\ =\hat{F}((e\left(k\right)+\tau ),(u_e\left(k\right)+{\hat{u}}_d\left(k\right)))-\tau +▿\hat{F}\left({\xi }_u\right){ϵ}_u\left(k\right)+{ϵ}_m\left(k\right),\end{array}$

其中， 为变换后的系统模型， 为神经网络系统模型；令τ为设定炉温，e(k)=x(k)-τ为k时刻的炉温误差，x(k)为k时刻的炉温；u_e(k)=u(k)-u_d(k)为k时刻变换炉系统运行过程中测量得到的实际输入量u(k)与额定输入量u_d(k)的差值；令 表示参考控制模型输出值，ε_m(k)为系统控制模型建模误差，ε_u(k)为参考控制模型建模误差；令 与ξ_u分别表示为

$▿\hat{F}\left({\xi }_u\right)=\frac{\partial \hat{F}((e\left(k\right)+\tau ),{\xi }_u)}{\partial {\xi }_u},$

${\xi }_u=c_u(u_e\left(k\right)+{\hat{u}}_d\left(k\right))+(1-c_u)(u_e\left(k\right)+{\hat{u}}_d\left(k\right)+{ϵ}_u\left(k\right)),$

其中0≤c_u≤1为常数。

7.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，在步骤S4中所建立的求解最优控制的函数如下所示：

$\left\{\begin{array}{c}U(e\left(k\right),u_e\left(k\right))=e^T\left(k\right)\mathrm{Qe}\left(k\right)+u_e^T\left(k\right){\mathrm{Ru}}_e\left(k\right)\\ J^{*}\left(e\left(k\right)\right)=\underset{u_e\left(k\right)}{\inf }\{U(e\left(k\right),u_e\left(k\right))+J^{*}\left(e(k+1)\right)\}\\ u_e^{*}\left(e\left(k\right)\right)=\arg \underset{u_e\left(k\right)}{\inf }\{U(e\left(k\right),u_e\left(k\right))+J^{*}\left(e(e+1)\right)\}\end{array}\right.,$

其中，U(e(k)，u_e(k))为效用函数，e(k)为系统状态误差，u_e(k)为系统输入误差，Q、R为正定矩阵，J^*(e(k))为最优性能指标函数， 为最优控制律。

8.如权利要求1所述的变换炉系统的炉温控制方法，其特征在于，在步骤S4中所建立的最优控制的函数如下求解：

步骤S4-1、令i=0，对 给定容许控制μ(e(k))，定义初始迭代性能指标函数：

V₀(e(k))=P(e(k))，

其中P(e(k))=U(e(k)，μ(e(k)))+P(e(k+1))；

步骤S4-2、根据初始迭代性能指标函数计算初始控制：

${\hat{u}}_0\left(e\left(k\right)\right)=\arg \underset{u_e\left(k\right)}{\min }\{U(e\left(k\right),u_e\left(k\right))+{\hat{V}}_0\left(e(k+1)\right)\}+{\rho }_0\left(e\left(k\right)\right),$

其中 迭代控制律公式中ρ₀(e(k))为初始情况下的有界控制迭代误差；

步骤S4-3、更新下一迭代性能指标函数，采用神经网络获得更新后的性能指标函数 表达式为：

${\hat{V}}_1\left(e\left(k\right)\right)=U(e\left(k\right),{\hat{u}}_0\left(e\left(k\right)\right))+{\hat{V}}_0\left(e(k+1)\right)+{\pi }_0\left(e\left(k\right)\right),$

公式中π₀(e(k))为初始有界性能指标函数迭代误差；

步骤S4-4、获得第i次迭代的系统控制，表达式为：

${\hat{u}}_i\left(e\left(k\right)\right)=\arg \underset{u_e\left(k\right)}{\min }\{U(e\left(k\right),u_e\left(k\right))+{\hat{V}}_i\left(e(k+1)\right)\}+{\rho }_i\left(e\left(k\right)\right),$

迭代控制律公式中ρ_i(e(k))为有界控制迭代误差；

步骤S4-5、使用神经网络函数逼近目标值获得下一迭代性能指标函数，表达式如下：

${\hat{V}}_{i+1}\left(e\left(k\right)\right)=U(e\left(k\right),{\hat{u}}_i\left(e\left(k\right)\right))+{\hat{V}}_i\left(e(k+1)\right)+{\pi }_i\left(e\left(k\right)\right),$

上式中π_i(e(k))为有界性能指标函数迭代误差；

可按下式获得性能指标函数的目标值：

$V_{i+1}\left(e\left(k\right)\right)=U(e\left(k\right),{\bar{u}}_i\left(e\left(k\right)\right))+{\hat{V}}_i\left(e(k+1)\right),$

其中${\bar{u}}_i\left(e\left(k\right)\right)=\arg \underset{u_e\left(k\right)}{\min }\{U(e\left(k\right),u_e\left(k\right))+{\hat{V}}_i\left(e(k+1)\right)\}$为控制目标函数；

步骤S4-6、将 带入到 表达式中获得 并通过数值比较的方式获得迭代性能指标函数 与性能指标函数目标值V_i+1(e(k))之间的误差σ≥1，满足：

${\hat{V}}_{i+1}\left(e\left(k\right)\right)\le \sigma V_{i+1}\left(e\left(k\right)\right);$

步骤S4-7、通过数值比较的方式获得求解出参数γ、δ，其中0<γ<∞、1≤δ<∞满足：

$P\left(\bar{F}(e\left(k\right),u_e\left(k\right))\right)\le \mathrm{\gamma U}(e\left(k\right),u_e\left(k\right)),$

V₀(e(k))≤δP(e(k))；

步骤S4-8、判断迭代性能指标函数 的收敛性；如果不等式

$\sigma \le 1+\frac{\delta -1}{\mathrm{\gamma \delta }}$

成立，那么性能指标函数收敛，并且迭代控制 为稳定控制，转到步骤S4-4继续计算，直到 则算法停止；否则，减小控制迭代误差ρ_i(e(k))与性能指标函数迭代误差π_i(e(k))使得计算精度增加，转到步骤S4-2重新求解迭代控制与迭代性能指标函数。

说明书

技术领域

本发明属于变换炉技术领域，具体涉及变换炉的炉温控制方法，特别是一种通过变换炉系统的运行数据对变换炉炉温进行自学习最优控制的方法。

背景技术

变换炉是一种重要的化工设备，是煤气化制甲醇、煤变换联合循环发电等系统中变换工序的核心设备。变换炉以来自水煤浆制气工序的水煤气为原料，利用催化剂提高变换反应速率将水煤气中的CO和H₂O转化为CO₂和H₂。其工作过程简述如下：来自气化工序的水煤气分为两股进入变换炉，一股是经中温换热器，预热后进入变换炉上段，另一股是作为激冷气直接进入变换炉中段，气体在变换炉内发生变换反应，COS水解反应等一系列复杂物理化学过程，最终生成甲醇合成工序所需的具有合适氢碳比的生成气。

变换炉具有工艺流程复杂、设备庞大、反应滞后、耦合严重等特点。一方面通过变换的主要工作机理分析变换炉的工作动态，另一方面要根据变换炉运行特性对变换炉温度等重要参数进行最优调控，优化变换炉运行，提高变换炉系统运行效率并避免不必要的事故发生。然而在实际生产过程中，变换炉设备庞大，炉内温度高，反应剧烈以及时滞现象严重等使得变换炉的数学机理模型难以建立，这给变换炉系统优化与控制带来极大的困难。在变换炉系统每日运行过程中都会存储大量的数据，因此基于变换炉系统的运行数据，设计一套有效的最优控制方案，使得变换炉系统能够智能调控在最优工作状态是变换炉控制技术发展亟需解决的问题。

发明内容

(一)要解决的技术问题

本发明所要解决的技术问题是利用变换炉系统运行数据与神经网络，构建变换炉系统神经网络模型以及参考控制神经网络模型，采用基于自适应动态规划的方法，最优化控制变换炉的炉温工作状态。

(二)技术方案

基于变换系统生产过程的运行数据，利用自适应动态规划理论，构建变换炉系统炉温控制神经网络模型、以及参考控制神经网络模型，综合考虑建模误差，采用迭代自适应动态规划方法获得系统最优控制方案，实现变换炉系统温度最优化运行。

具体来说，本发明提出一种变换炉系统的炉温自学习控制方法，其包括：

S1、根据变换炉系统实际运行数据构建一个三层反向传播神经网络炉温控制模型，该炉温控制模型的输入为当前时刻原料中CO、CO₂、H₂和H₂O的输入流量，输出为当前时刻生成物中CO、CO₂、H₂和H₂O的输出流量，状态参数为当前时刻与下一时刻变换炉的炉温；

S2、根据所述变换炉系统实际运行数据构建一个三层反向传播神经网络参考控制模型，该参考控制模型的输入为当前时刻炉温和下一时刻的炉温，输出为当前时刻原料中CO、CO₂、H₂和H₂O的输入流量；

S3、将当前实际炉温与额定炉温之间的差作为系统状态误差，将当前实际输入流量和额定输入流量之间的差作为输入流量控制误差，根据所述炉温模型和参考控制模型，得到与输入流量控制误差相关的炉温误差函数；

S4、基于迭代自适应动态规划最优控制方法，根据所述炉温误差函数求解出最优输入流量控制误差函数，获得最优的变换炉炉温控制输入量。

根据本发明的具体实施方式，在步骤S1中构建的所述炉温控制模型表示为：

x^(k+1)=F^(x(k),u(k))=W^m1T(k)σ1(z(k))y^(k)=G^(x(k),u(k))=W^m2T(k)σ2(z(k)),]]>

其中， 为神经网络系统函数， 为变换炉系统炉温模型的神经网络权值， 为变换炉系统输出模型的神经网络权值，z(k)=[x^T(k)，u^T(k)]^T为构建所述变换炉炉温系统模型使用的神经网络的输入， 时刻变换炉炉温系统模型的炉温值， 为k时刻变换炉炉温系统模型的输出，x(k)为k时刻实际的炉温，u(k)为k时刻实际的组分输入流量，σ(·)为训练系统控制模型使用的神经网络双极S型激活函数，如下表示：

[σ(z)]i=ezi-e-ziezi+e-zi.]]>

根据本发明的具体实施方式，在步骤S1中所述神经网络权值 和 通过如下训练更新得到：

W^m1j+1(k+1)=W^m1j(k)-lm1σ1(z(k))x~jT(k+1)W^m2j+1(k+1)=W^m2j(k)-lm2σ2(z(k))y~jT(k),]]>

其中，l_m1>0，l_m2>0为神经网络的学习率， 为k+1时刻根据所述变换炉炉温系统模型得到的炉温 和变换炉系统运行过程中测量得到的实际炉温的差值， 为k+1时刻根据所述变换炉炉温系统模型得到的输出 和变换炉系统运行过程中测量得到的实际输出y(k)的差值。

根据本发明的具体实施方式，在步骤S2中所述参考控制模型如下所示：

u^f(k)=F^u(x(k),x(k+1))=W^uT(k)σu(zu(k)),]]>

其中， 表示参考控制模型的输出， 表示参考控制函数， 为参考控制模型神经网络权值，z_u(k)=[x^T(k)，x^T(k+1)]^T为参考控制模型输入，x(k)为k时刻的实际炉温，x(k+1)为k+1时刻的实际炉温，σ_u(·)为训练参考控制模型使用的神经网络双极S型激活函数，如下表示：

σu(z)=ez-e-zez+e-z.]]>

根据本发明的具体实施方式，在步骤S2中所述参考控制模型权值更新如下：

W^uj+1(k)=W^uj(k)-luσu(zu(k))u~fj(k),]]>

其中，l_u>0为神经网络学习率， 为k时刻所述参考控制模型的输出 和变换炉系统运行过程中测量得到的实际输入量u(k)的差值。

根据本发明的具体实施方式，在步骤S3中转化后的变换炉炉温使用如下所示的误差函数e(k)表示：

e(k+1)=F‾(e(k),ue(k))=F^((e(k)+τ),(ue(k)+u^d(k)))-τ+▿F^(ξu)ϵu(k)+ϵm(k),]]>

其中， 为变换后的系统模型， 为神经网络系统模型；令τ为设定炉温，e(k)=x(k)-τ为k时刻的炉温误差，x(k)为k时刻的炉温；u_e(k)=u(k)-u_d(k)为k时刻变换炉系统运行过程中测量得到的实际输入量u(k)与额定输入量u_d(k)的差值；令 表示参考控制模型输出值，ε_m(k)为系统控制模型建模误差，ε_u(k)为参考控制模型建模误差；令 与ξ_u分别表示为

▿F^(ξu)=∂F^((e(k)+τ),ξu)∂ξu,]]>

ξu=cu(ue(k)+u^d(k))+(1-cu)(ue(k)+u^d(k)+ϵu(k)),]]>

其中0≤c_u≤1为常数。

根据本发明的具体实施方式，在步骤S4中所建立的求解最优控制的函数如下所示：

U(e(k),ue(k))=eT(k)Qe(k)+ueT(k)Rue(k)J*(e(k))=infue(k){U(e(k),ue(k))+J*(e(k+1))}ue*(e(k))=arginfue(k){U(e(k),ue(k))+J*(e(e+1))},]]>

其中，U(e(k)，u_e(k))为效用函数，e(k)为系统状态误差，u_e(k)为系统输入误差，Q、R为正定矩阵，J^*(e(k))为最优性能指标函数， 为最优控制律。

根据本发明的具体实施方式，在步骤S4中所建立的最优控制的函数如下求解：

步骤S4-1、令i=0，对 给定容许控制μ(e(k))，定义初始迭代性能指标函数：

V₀(e(k))=P(e(k))，

其中P(e(k))=U(e(k)，μ(e(k)))+P(e(k+1))；

步骤S4-2、根据初始迭代性能指标函数计算初始控制：

u^0(e(k))=argminue(k){U(e(k),ue(k))+V^0(e(k 一种变换炉系统的炉温自学习控制方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。