专利摘要

专利摘要

本发明公开了一种任意量子比特门的分解方法，属于量子态的操控技术领域。所述方法包括：将任意n量子比特门U分解为多个连续的Cn(U)，通过构造基本段和修正段并利用嵌套递推的方式，分别采用线路复杂度为O(2n)的指数分解方式和线路复杂度为O(n2)的多项式分解方式来实现对任意量子比特门的分解。本发明实现了将任意量子比特门分解为复杂度分别为量子位指数形式和多项式形式，准确地给出了只含有两量子比特受控非门和单量子比特门的量子线路图和相应解析表达式，从而在量子态的传输过程中实现了对量子态的任意操作；计算出了两种分解形式所需的基本逻辑门的数目；在分解的结果中使用相移近似门代替Toffoli门，极大地降低了线路的复杂度。

权利要求

1.一种任意量子比特门的分解方法，其特征在于，所述方法包括：

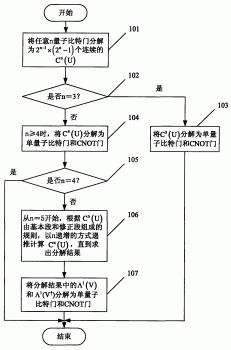
步骤1：将任意n量子比特门分解为多个连续的n量子比特完全受控U门Cⁿ(U)；

步骤2：当n＝3时，将所述n量子比特完全受控U门C³(U)分解为单量子比特门和两量子比特受控非门，然后结束；

步骤3：当n≥4时，将4量子比特完全受控U门C⁴(U)分解为单量子比特门和两量子比特受控非门；如果n＝4，则结束；否则，执行步骤4；

步骤4：从n＝5开始，根据所述Cⁿ(U)由基本段和修下段组成的规则，以n递增的方式递推计算Cⁿ(U)，直到求出所述Cⁿ(U)的分解结果，所述基本段由根据n-1量子比特完全受控U门C^n-1(U)得到，所述修正段由根据两量子比特受控V门Λ¹(V)、两量子比特受控V^门Λ¹(V^)和两量子比特受控非门得到，所述V为按照预设的变形规则对所述U进行变形得到，然后将所述分解结果中的C⁴(U)、Λ¹(V)和Λ¹(V^)分别分解为单量子比特门和两量子比特受控非门，结束。

2.根据权利要求1所述的任意量子比特门的分解方法，其特征在于，所述步骤4中所述基本段由根据n-1量子比特完全受控U门C^n-1(U)得到的步骤具体为：

在n-1量子比特完全受控U门C^n-1(U)的最后两位之间附加1个量子位，得到所述基本段。

3.根据权利要求1所述的任意量子比特门的分解方法，其特征在于，所述步骤4中所述修正段由根据两量子比特受控V门Λ¹(V)、两量子比特受控V^门Λ¹(V^)和两量子比特受控非门得到的步骤具体包括：

将1个两量子比特受控V门Λ¹(V)、1个两量子比特受控V^门Λ¹(V^)和3个两量子比特受控非门组成第一阵列块；

将1个两量子比特受控V门Λ¹(V)、1个两量子比特受控V^门Λ¹(V^)和1个两量子比特受控非门组成第二阵列块；

将2^n-2个所述第一阵列块和2^n-2个所述第二阵列块交替排列组成所述修正段。

4.根据权利要求1所述的任意量子比特门的分解方法，其特征在于，所述步骤4中预设的变形规则具体为：$V^{2^{n-2}}=U.$

5.一种任意量子比特门的分解方法，其特征在于，所述方法包括：

步骤1：将任意n量子比特门分解为多个连续的n量子比特完全受控U门Cⁿ(U)；

步骤2：当n＝3时，将所述n量子比特完全受控U门C³(U)分解为单量子比特门和两量子比特受控非门，然后结束；

步骤3：当n≥4且n＜6时，将4量子比特完全受控U门C⁴(U)分解为单量子比特门和两量子比特受控非门；如果n＝4，则结束；否则，执行步骤4；

步骤4：从n＝5开始，根据所述Cⁿ(U)由基本段和修正段组成的规则，以n递增的方式递推计算Cⁿ(U)，直到求出所述Cⁿ(U)的分解结果，所述基本段由根据n-1量子比特完全受控U门C^n-1(U)得到，所述修正段由根据两量子比特受控V门Λ¹(V)、两量子比特受控V^门Λ¹(V^)和两量子比特受控非门得到，所述V为按照预设的第一变形规则对所述U进行变形得到；然后将所述分解结果中的C⁴(U)、Λ¹(V)和Λ¹(V^)分别分解为单量子比特门和两量子比特受控非门，结束；

步骤5：当n≥6时，将6量子比特完全受控U门C⁶(U)分解为两量子比特受控非门、托弗里门和两量子比特受控门，所述两量子比特受控门包括Λ¹(V₁)、Λ¹(V₂)、Λ¹(V₃)、Λ¹(V₄)、Λ¹(V₁^)、Λ¹(V₂^)、Λ¹(V₃^)和Λ¹(V₄^)，所述V₁、V₂、V₃和V₄为按照预设的第二变形规则对所述U进行变形得到；如果n＝6，则结束；否则，执行步骤6；

步骤6：从n＝7开始，按照预设的第三变形规则以及所述Cⁿ(U)由基本段和修正段组成的规则，以n递增的方式递推计算Cⁿ(U)，直到求出所述Cⁿ(U)的分解结果，所述基本段由根据n-1量子比特完全受控V₁门C^n-1(V₁)得到，所述C^n-1(V₁)由所述C^n-1(U)得到，所述修正段由根据两量子比特受控V₁门Λ¹(V₁)、两量子比特受控V₁^门Λ¹(V₁^)和托弗里门得到；所述分解结果中包括两量子比特受控非门、Λ¹(V₁)、Λ¹(V₂)、…、Λ¹(V_n-2)和Λ¹(V₁^)、Λ¹(V₂^)、…、Λ¹(V_n-2^)和托弗里门，然后执行步骤7；

步骤7：将所述步骤6中的分解结果中的Λ¹(V₁)、Λ¹(V₂)、…、Λ¹(V_n-2)和Λ¹(V₁^)、Λ¹(V₂^)、…、Λ¹(V_n-2^)分别分解为单量子比特门和两量子比特受控非门；将所述步骤6中的分解结果中的托弗里门分解为单量子比特门和两量子比特受控非门，然后结束。

6.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤4中所述基本段由根据n-1量子比特完全受控U门C^n-1(U)得到的步骤具体为：

在n-1量子比特完全受控U门C^n-1(U)的最后两位之间附加1个量子位，得到所述基本段。

7.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤4中所述修正段由根据两量子比特受控V门Λ¹(V)、两量子比特受控V^门Λ¹(V^)和两量子比特受控非门得到的步骤具体包括：

将1个两量子比特受控V门Λ¹(V)、1个两量子比特受控V^门Λ¹(V^)和3个两量子比特受控非门组成第一阵列块；

将1个两量子比特受控V门Λ¹(V)、1个两量子比特受控V^门Λ¹(V^)和1个两量子比特受控非门组成第二阵列块；

将2^n-2个所述第一阵列块和2^n-2个所述第二阵列块交替排列组成所述修正段。

8.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤4中预设的第一变形规则具体为：$V^{2^{n-2}}=U.$

9.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤5中预设的第二变形规则具体包括：$V_1^2=U,$$V_2^2=V_1,$$V_3^2=V_2,$$V_4^2=V_3.$

10.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤6中预设的第三变形规则具体为：$V_{n-2}^2=V_{n-3}.$

11.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤6中所述基本段由根据n-1量子比特完全受控V₁门C^n-1(V₁)得到，所述C^n-1(V₁)由所述C^n-1(U)得到的步骤具体包括：

将所述C^n-1(U)中的V₁、V₂、...、V_n-3分别替换为V₂、V₃、...、V_n-2，得到n-1量子比特完全受控V₁门C^n-1(V₁)，所述V_n-2为利用所述第三变形规则计算得到的；

在所述C^n-1(V₁)的最后两位之间附加1个量子位，得到所述基本段。

12.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤6中所述修正段由根据两量子比特受控V₁门Λ¹(V₁)、两量子比特受控V₁^门Λ¹(V₁^)和托弗里门得到的步骤具体包括：

根据量子位n设置第一周期和第二周期；

将呈现两个所述第一周期排列的托弗里门组成第一阵列块；

将呈现两个所述第二周期排列的托弗里门组成第二阵列块；

所述每个周期内的托弗里门均以固定的对称轴为中心呈轴对称排列；

将两量子比特受控V₁门Λ¹(V₁)、两量子比特受控V₁^门Λ¹(V₁^)、所述第一阵列块和第二阵列块组成所述n量子比特完全受控门的修正段。

13.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤7中将所述步骤6中的分解结果中的托弗里门分解为单量子比特门和两量子比特受控非门的步骤具体包括：

将所述步骤6中的分解结果中的每个托弗里门，分解为2个两量子比特受控非门和3个两量子比特受控门；

将所述每个两量子比特受控门分解为2个两量子比特受控非门和4个单量子比特门。

14.根据权利要求5所述的任意量子比特门的分解方法，其特征在于，所述步骤7中将所述步骤6中的分解结果中的托弗里门分解为单量子比特门和两量子比特受控非门的步骤具体包括：

将所述步骤6中的分解结果中的托弗里门中的多个托弗里门，用相移近似托弗里门代替；

将所述每个相移近似托弗里门分解为3个两量子比特受控非门和4个单量子比特门；

将所述步骤6中的分解结果中除替换为相移近似托弗里门外的其余每个托弗里门，分解为2个两量子比特受控非门和3个两量子比特受控门；

将所述每个两量子比特受控门分解为2个两量子比特受控非门和4个单量子比特门。

说明书

技术领域

本发明涉及量子态的操控技术领域，特别涉及一种任意量子比特门的分解方法。

背景技术

量子计算和量子通信是量子物理学与计算机科学、信息科学相结合而产生的一门新型交叉学科。近一、二十年来，量子信息论在理论和实验上都有着相当迅速的发展，取得了令人惊喜的研究成果并显示出十分广阔的科学技术应用前景。在量子信息理论中，量子信息的基本单位是量子比特(qubit)，一个量子比特可以同时处于量子态|0>和|1>的任意复系数组成的线性叠加态|ψ>＝α|0>+β|1>上。一个量子比特就是一个二维希尔伯特(Hilbert)空间，它比经典比特承载更多的信息。

在量子信息学中，量子态的制备和操控通过多种量子逻辑门来实现。n个量子比特量子逻辑门可以用2ⁿ×2ⁿ的矩阵形式表示。量子逻辑门相应矩阵U必须满足酉性(幺正性，unitary)，即UU^＝I，其中U^是U的共轭转置(由U的转置和复共轭得到)，I是2ⁿ×2ⁿ的单位矩阵。单量子比特逻辑门由2×2的酉矩阵给出，例如泡利(Pauli)矩阵：

$X=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),$$Y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),$$Z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right);$(1)

量子比特有一个非常有用的图像是几何表示：|ψ>可以写为 其中θ，，γ都是实数，e^iγ是整体相位。数θ，定义了三维单位球面上的一个点，这个球面称为--布洛赫(Bloch)球面。一组重要的量子操作是定义在布洛赫球面上关于 轴的旋转算子：

$R_x\left(\mathrm{\θ}\right)=\left(\begin{array}{cc}\cos \frac{\mathrm{\θ}}{2}& -i\sin \frac{\mathrm{\θ}}{2}\\ -i\sin \frac{\mathrm{\θ}}{2}& \cos \frac{\mathrm{\θ}}{2}\end{array}\right),$$R_y\left(\mathrm{\θ}\right)=\left(\begin{array}{cc}\cos \frac{\mathrm{\θ}}{2}& -\sin \frac{\mathrm{\θ}}{2}\\ \sin \frac{\mathrm{\θ}}{2}& \cos \frac{\mathrm{\θ}}{2}\end{array}\right),$$R_z\left(\mathrm{\θ}\right)=\left(\begin{array}{cc}{e}^{-\mathrm{i\θ}/2}& 0\\ 0& e^{\mathrm{i\θ}/2}\end{array}\right).$(2)

一类重要的量子逻辑门是完全受控单量子比特门(fully controlled single-qubit gate)。它的特征是：在n量子比特的体系中有n-1个量子比特作为控制量子位(control qubit)，1个量子比特作为目标量子位(target qubit)。当这n-1个控制量子位的逻辑值x₁，...x_n-1∈{0，1}取某一组确定的数值时，目标量子位进行酉操作U；否则目标量子位保持不变。逻辑值为0的控制量子位称为置0有效控制位，逻辑值为1的量子位称为置1有效控制位。完全受控单量子比特门中一种特殊的受控门是Λ^m(U)门(也记作C^m+1(U)门)。对于任意酉矩阵$U=\left(\begin{array}{cc}{u}_{00}& u_{01}\\ u_{10}& u_{11}\end{array}\right)$和m∈{0，1，2，...}，Λ^m(U)有m个控制量子位为x₁，...，x_m，1个目标量子位y，它的作用可以表示为

${\mathrm{\Λ}}^m\left(U\right)\left(\right|x_1,...x_m,y\⟩)=\left\{\begin{array}{ccc}{u}_{y0}|x_1,...x_m,0\⟩+u_{y1}|x_1,...x_m,1\⟩& \mathrm{if}& {^}_{k=1}^m{x}_k=1\\ |x_1,...x_m,y\⟩& \mathrm{if}& {^}_{k=1}^m{x}_k=0\end{array}\right.,---\left(3\right)$

其中，x₁，...x_m，y∈{0，1}，∧_k＝1^mx_k表示{x_k}之间的逻辑与值。当且仅当m个控制量子位x₁，...，x_m的值都为1时，目标量子位进行酉操作U；否则所有值不变。n量子比特完全受控量子门，可以由Λ^n-1(U)门在置0有效控制位前后各加一个X操作来实现，例如图1中所示的情况。几种特殊情况：

1.当m＝0，Λ⁰(U)就是U；

2.当m＝1，$U=X=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$时，对应两量子比特受控非门(CNOT gate)；

3.当m＝1时，对于任意单量子比特门$U=\left(\begin{array}{cc}{e}^{i(\mathrm{\α}-\mathrm{\β}/2-\mathrm{\δ}/2)}\cos \frac{\mathrm{\γ}}{2}& -e^{i(\mathrm{\α}-\mathrm{\β}/2+\mathrm{\δ}/2)}\sin \frac{\mathrm{\γ}}{2}\\ e^{i(\mathrm{\α}+\mathrm{\β}/2-\mathrm{\δ}/2)}\sin \frac{\mathrm{\γ}}{2}& e^{i(\mathrm{\α}+\mathrm{\β}/2+\mathrm{\δ}/2)}\cos \frac{\mathrm{\γ}}{2}\end{array}\right),$如图2所示，Λ¹(U)可以分解为2个CNOT门和4个单量子比特门。其中，A＝R_z(β)R_y(γ/2)，B＝R_y(-γ/2)R_z(-(α+β)/2)，C＝R_z((δ-β)/2)，$\mathrm{\Φ}=\left(\begin{array}{cc}{e}^{\mathrm{i\δ}}& 0\\ 0& e^{\mathrm{i\δ}}\end{array}\right),$$E=\left(\begin{array}{cc}1& 0\\ 0& e^{\mathrm{i\δ}}\end{array}\right),$如图3所示。

4.当m＝2时，对应托弗里门(Toffoli gate)。1995年，巴兰科等人提出了Toffoli门最基本的精确分解方法(A.Barenco et.al.，“Elementary gates for quantum computation”，Phys.Rev.A52，3457，1995)。如图4所示，此方法将Toffoli门精确分解为6个CNOT门和8个单量子比特门。1994年，蒂文森佐和施莫林用相移近似(Congruent Modulo Phase Shifts)方法模拟Toffoli门(D.P.DiVincenzo and J.Smolin，“Results on two-bit gate design for quantum computers”，inProceedings of the Workshop on Physics and Computation，PhysComp’94，p.14)，称为相移近似Toffoli门。最重要的一种相移近似Toffoli门如图5所示，此线路可以表示为：

其中R_c表示为对第c个量子比特进行的R_y(π/4)操作。此种相移近似Toffoli门的作用可表示为$|c_1,c_2,t\⟩\→{(-1)}^{c_1\stackrel{\‾}{c_2}t}|c_1,c_2,t\⊕c_1{c}_2\⟩,$即它与Toffoli门的差别仅在于对|101>施加了一个幅角为π的相对相位。它仅需要3个CNOT门和4个单量子比特门。

如果用一组门的量子线路可以以任意精度近似任意的酉运算，则称这组门对量子计算是通用的。首先，两级酉门(two-level unitary gate，只不平凡地作用在两个分量组成的自空间上，而对余空间内其他分量均不变的酉矩阵)对于量子计算是通用的。n量子比特系统，任意酉矩阵可以写为至多2^n-1(2ⁿ-1)个两级酉矩阵的乘积。单量子比特门和两量子比特受控非门对于量子计算是通用的，通常用单量子比特门和受控非门的个数来标志一个量子线路或者量子算法的复杂程度，称作复杂度(complexity)。在量子计算的算法中，同一问题可用不同量子线路解决，而一个量子线路的质量优劣将影响到算法乃至程序的效率。一个量子线路或者量子算法的评价主要从复杂度来考虑。一般来说，复杂度越低，量子线路的质量越优，量子计算的性能越好。这是因为：一方面，实际的量子计算过程所需的纠缠(entanglement)特性必须依赖各个量子比特之间的相干作用(coherence interaction)，而量子系统不可避免地与外界环境发生退相干(decoherence)作用，也就是说量子操作必须在系统的所允许的相干时间内完成。而量子线路的复杂度决定了系统的能否在系统的最大相干时间内完成量子操作。另一方面，量子线路的复杂度决定了量子算法的弛豫时间，复杂度越低，弛豫时间越短，计算的性能越好。因此，利用合适的分解方法来降低复杂度的目的在于改进实际的量子算法。这对多种物理系统，例如，核磁共振(NMR)、量子点、离子阱、半导体硅基、约瑟夫森结等的多种量子计算物理过程，例如，量子态进行制备、操控、存储和传送来说尤为重要。要降低复杂度，涉及到量子门的合并及量子线路图的简化。这里举例说明其中几种最为重要的量子线路简化方法：1.连续的单量子比特门可以合并为一个；2.任意连续的3个CNOT门即可化简为2个CNOT门，如图6所示；3.利用如图3所示的单量子比特门E和CNOT门的对易关系(量子力学两个算符对易关系反映在量子线路中，即是对应的两个量子门的位置可以调换)，合并相邻的单量子比特门和CNOT门等。

现有技术中，对于任意n量子比特门的分解，迄今为止最被人们认可的分解方式就是将具有4ⁿ个自由度的酉矩阵分解成2^n-1(2ⁿ-1)个两级酉门。但是，该技术仍然不能解决如何将两级酉门分解成更简单的单量子比特门和受控非门的问题，因此在量子态的传输过程中也无法实现对量子态的任意操作。

另外一种对于任意n量子比特门的分解方案为2004年芬兰的瓦替艾林等人(J.J.Vartiainen，M.Mottonen，M.M.Salomaa)提出的，以一种使用2^n-1(2ⁿ-1)个完全受控门来实现任意n量子比特门的量子线路图(J.J.Vartiainen，M.Mottonen and M.M.Salomaa，“EfficientDecomposition of Quantum Gates”，Phys.Rev.Lett.92，177902，2004)。不妨简称该方案为VMS04方案。此方案通过使用一组按格雷码(Gray Code，格雷码是一组具有回文顺序的二进制数列，n比特的由2ⁿ个n比特二进制数列组成，序列中相邻两个二进制数只有一位的数值是不同的)编码的基矢，可以将任意一个两级酉门等价为一个完全受控门。因此，运用VMS04方案，任意一个n量子比特门只需O(4ⁿ)个完全受控门就可以实现。首先，VMS04方案的过程为：n比特的量子寄存器的状态通常用N维希尔伯特空间当中的态|Ψ>来表示，其中N＝2ⁿ。在选定的一组基{|e_k>}下，n量子比特门可以用2ⁿ×2ⁿ的矩阵U表示。利用吉文斯旋转(Givens Rotation)对矩阵U进行类似正交上三角分解(QR decompostion)的过程，可以将任意酉矩阵转化为单位矩阵I₂ⁿ。作用在矩阵A上的吉文斯旋转定义为：ⁱG_j，k＝G_j，k(A)，吉文斯旋转ⁱG_j，k是一个两级酉矩阵，它只在基矢|e_j>和|e_j>组成的自空间上非奇异，而对其它的基矢没有作用。定义作用在矩阵$A={\{a_{1,n}\}}_{1,n=1}^N$上的${{}^{i}G_{j,k}=\left\{g_{1,n}\right\}}_{1,n=1}^N$中表示为：

${}^i\mathrm{\Γ}_{j,k}:=\left(\begin{array}{cc}{}^{i}g_{k,k}& {}^{i}g_{k,j}\\ {}^{i}g_{j,k}& {}^{i}g_{j,j}\end{array}\right)=\frac{1}{\sqrt{{\left|a_{j,i}\right|}^2+{\left|a_{k,i}\right|}^2}}\left(\begin{array}{cc}{a}_{k,i}^{*}& a_{j,i}^{*}\\ -a_{j,i}& a_{k,i}\end{array}\right).---\left(5\right)$

即矩阵ⁱG_j，k只在第j，k行和第j，k列四个位置上有非奇异元素，其他元素与单位矩阵I₂ⁿ一致。

在n量子比特的计算当中，以往方案中通常选取的是按照二进制数依次递增的一组基矢$\left(\mathrm{BCB}\right)|e_k\⟩={\⊗}_i|x_i^k\⟩,$其中$x_i^k\∈\left\{\mathrm{0,1}\right\}.$K和i分别标志基矢和量子位，其中k＝1，...，2ⁿ，i＝1，...n，$k=1+{\mathrm{\Σ}}_{i=0}^n{2}^i{x}_i^k.$而在VMS04方案中，选取一组按照格雷码排列的基矢(GCB)。假设一组n量子比特的格雷码为{c₁ⁿ，c₂ⁿ，...，c₂ⁿⁿ}，其中相邻元素c_iⁿ和c_i+1ⁿ之间只有一位的数值不同。设c_iⁿ的二进制表示为$c_i^k=b_n^i...b_2^i{b}_1^i,$i的二进制表示为i_b，格雷码排列的基矢$c_i^n=i_b\mathrm{XOR}(i_b/2).$另外，设函数γ(i)表示c_iⁿ

任意量子比特门的分解方法专利购买费用说明

Q：办理专利转让的流程及所需资料

A：专利权人变更需要办理著录项目变更手续，有代理机构的，变更手续应当由代理机构办理。

1：专利变更应当使用专利局统一制作的“著录项目变更申报书”提出。

2：按规定缴纳著录项目变更手续费。

3：同时提交相关证明文件原件。

4：专利权转移的，变更后的专利权人委托新专利代理机构的，应当提交变更后的全体专利申请人签字或者盖章的委托书。

Q:专利著录项目变更费用如何缴交

A：（1）直接到国家知识产权局受理大厅收费窗口缴纳,（2）通过代办处缴纳，（3）通过邮局或者银行汇款,更多缴纳方式

Q：专利转让变更，多久能出结果

A：著录项目变更请求书递交后，一般1-2个月左右就会收到通知，国家知识产权局会下达《转让手续合格通知书》。